
 已知:如图,点B(3,3)在双曲线y=$\frac{k}{x}$(其中x>0)上,点D在双曲线y=$\frac{-4}{x}$ (其中x<0)上,点A、C分别在x、y轴的正半轴上,且点A、B、C、D围成的四边形为正方形.
已知:如图,点B(3,3)在双曲线y=$\frac{k}{x}$(其中x>0)上,点D在双曲线y=$\frac{-4}{x}$ (其中x<0)上,点A、C分别在x、y轴的正半轴上,且点A、B、C、D围成的四边形为正方形.分析 (1)把B的坐标代入求出即可;
(2)过D作DE⊥x于点E,过点B作BF⊥x于点F,证△DAE≌△ABF,推出DE=AF=3-a,AE=FB=3,OE=3-a,从而求得D的坐标(a-3,3-a),代入y=$\frac{-4}{x}$ 即可求得a的值.
解答 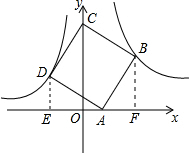 解:(1)∵点B(3,3)在双曲线y=$\frac{k}{x}$(其中x>0)上,
解:(1)∵点B(3,3)在双曲线y=$\frac{k}{x}$(其中x>0)上,
∴3=$\frac{k}{3}$
∴k=3×3=9;
(2)过D作DE⊥x于点E,过点B作BF⊥x于点F,
则∠DEA=∠AF B=90°,
∵点B(3,3),
∴BF=3,OF=3,
∵A的坐标为(a,0),
∴OA=a,AF=3-a,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAE+∠BAF=90°,
又∵∠DAE+∠ADE=90°,
∴∠ADE=∠BAF
在△DAE和△ABF中,
$\left\{\begin{array}{l}{∠DEA=∠AFB}\\{∠ADE=∠BAF}\\{AD=AB}\end{array}\right.$,
∴△DAE≌△ABF(AAS),
∴DE=AF=3-a,AE=FB=3,
∴OE=3-a,
又∵点D在第二象限,
∴D(a-3,3-a);
∵点D在双曲线y=$\frac{-4}{x}$ (其中x<0)上,
∴3-a=$\frac{-4}{a-3}$,
∴a=1或a=5(不合题意,舍去),
∴a=1.
点评 本题考查了正方形的性质,反比例函数图象上点的坐标特征,全等三角形的性质和判定的应用,主要考查学生运用性质进行推理和计算的能力,题目比较好,难度适中.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com