
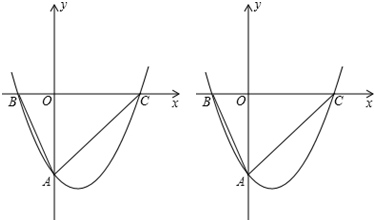
���� ��1��ֻ�����ô���ϵ��������A��B����������������ߵĽ���ʽ�����ɽ�����⣻
��2�����ȸ���ƽ��������ʾ���ƶ���ĺ�������ʽ��������m��ʾ���ú����Ķ������꣬��ͼ1���������ֱ��AB��AC�Ľ���ʽ�У�����ȷ��P�ڡ�ABC��ʱm��ȡֵ��Χ��
��3�����ٵ���P��ֱ��AC�·�ʱ����PH��y�ᣬ��x����H����AC��D����ͼ2����P��x��$\frac{1}{2}$x2-x-4������D��x��x-4�����Ӷ���PD=x-4-��$\frac{1}{2}$x2-x-4��=-$\frac{1}{2}$ ��x-2��2+2���ɵ�S=S��PDA+S��PDC=$\frac{1}{2}$PD��OC=-��x-2��2+4����Ȼx=2ʱ��S���Ϊ4����O��S��4���ڵ���P��ֱ��AC�Ϸ�ʱ����ͼ3����O��S��12�����ݢ١��ڼ��ɵõ���S=4��Ӧ�ĵ�P����ֻ��2����
��4���ٵ���M�ڵ�C���ұ�ʱ��ȡOC�е�E������AE����ͼ4������OE=OB=2�����ݴ�ֱƽ���ߵ����ʿɵ�AB=AE�����ݵ��������ε����ʿɵá�BAO=��EAO���Ӷ��õ���EAO+��CAE=��BAO+��CAE=45�㣮��������OMA+��OAB=��ACB=45��ɵá�OMA=��CAE���Ӷ��ɵá�AEC�ס�MEA���������������ε����ʼ������ME���Ӷ����BM���ڵ���M�ڵ�C�����ʱ��ȡOC�е�E������AE����ͼ5��ͬ�������BM��ֵ��
��� �⣺��1����A��0��-4����B��-2��0������������y=$\frac{1}{2}$x2+bx+c�У��ã�
$\left\{\begin{array}{l}{c=-4}\\{\frac{1}{2}��4-2b+c=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=-1}\\{c=-4}\end{array}\right.$��
�������ߵĽ���ʽy=$\frac{1}{2}$x2-x-4��
��2��m��ȡֵ��ΧΪ0��m��$\frac{5}{2}$��
��ʾ������ɵã��������ߵĽ���ʽΪ��y=$\frac{1}{2}$��x+m��2-��x+m��-4+$\frac{7}{2}$��
��y=$\frac{1}{2}$��x+m-1��2-1����P������Ϊ��1-m��-1������ͼ1��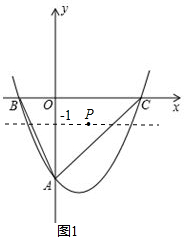
�ɣ�1���������߽���ʽ�ɵã�C��4��0����
���ô���ϵ�������ֱ��AC�Ľ���ʽΪy=x-4��ֱ��AB�Ľ���ʽΪy=-2x-4��
����P��ֱ��AB��ʱ��-2��1-m��-4=-1����ã�m=$\frac{5}{2}$
����P��ֱ��AC��ʱ����1-m��-4=-1����ã�m=-2��
�൱��P�ڡ�ABC��ʱ��-2��m��$\frac{5}{2}$
�֡�m��0��
��0��m��$\frac{5}{2}$��
��3���ٵ���P��ֱ��AC�·�ʱ��
��PH��y�ᣬ��x����H����AC��D����ͼ2��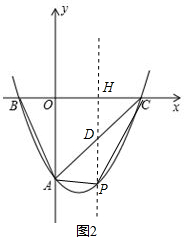
��P��x��$\frac{1}{2}$x2-x-4������D��x��x-4����
��PD=x-4-��$\frac{1}{2}$x2-x-4��=-$\frac{1}{2}$ ��x-2��2+2
��S=S��PDA+S��PDC=$\frac{1}{2}$PD•OH+$\frac{1}{2}$PD•HC
=$\frac{1}{2}$PD��OC=2PD
=-��x-2��2+4
��x=2ʱ��S���Ϊ4��
��0��S��4��
���ͼ���֪����0��S��4ʱ��ÿȡһ��Sֵ����Ӧ�ĵ�P����ֻ��2����
��S=4ʱ����Ӧ�ĵ�P����ֻ��1����
�ڵ���P��ֱ��AC�Ϸ�ʱ����ͼ3��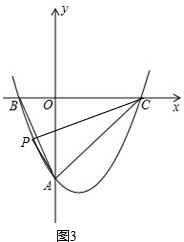
��S��ABC=$\frac{1}{2}$BC•OA=$\frac{1}{2}$��6��4=12��
��O��S��12��
���ͼ���֪����0��S��12ʱ��ÿȡһ��Sֵ����Ӧ�ĵ�P����ֻ��1����
��������������P��x���·�ʱ��0��S��4ʱ��Ӧ�ĵ�P����ֻ��2����
��4���ٵ���M�ڵ�C���ұ�ʱ��
ȡOC�е�E������AE����ͼ4��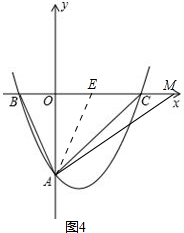
����OE=OB=2��
��OA��BE��
��AB=AE��
���BAO=��EAO��
��OA=OC����AOC=90�㣬
���OAC=��OCA=45�㣬
���EAO+��CAE=45�㣬
���BAO+��CAE=45�㣮
�ߡ�OMA+��OAB=��ACB=45�㣬
���OMA=��CAE��
�ߡ�AEC=��MEA��
���AEC�ס�MEA��
��$\frac{AE}{ME}$=$\frac{EC}{EA}$��
��AE=$\sqrt{O{A}^{2}+O{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$��EC=4-2=2��
��$\frac{2\sqrt{5}}{ME}$=$\frac{2}{2\sqrt{5}}$��
��ME=10��
��BM=BE+ME=4+10=14��
�ڵ���M�ڵ�C�����ʱ��ȡOC�е�E������AE����ͼ5��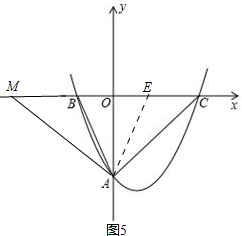
ͬ���ɵã�BM=10��
����������BM=14��10��
���� ������Ҫ�������ô���ϵ��������κ�����һ�κ����Ľ���ʽ����ֱƽ���ߵ����ʡ����������ε����ʡ����������ε��ж������ʡ����ɶ�����֪ʶ���ڽ������Ĺ������õ��������ۡ����ν�ϡ�������ٽ�ֵ������Ҫ����ѧ˼�뷽����Ӧ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ����B��3��3����˫����y=$\frac{k}{x}$������x��0���ϣ���D��˫����y=$\frac{-4}{x}$ ������x��0���ϣ���A��C�ֱ���x��y����������ϣ��ҵ�A��B��C��DΧ�ɵ��ı���Ϊ�����Σ�
��֪����ͼ����B��3��3����˫����y=$\frac{k}{x}$������x��0���ϣ���D��˫����y=$\frac{-4}{x}$ ������x��0���ϣ���A��C�ֱ���x��y����������ϣ��ҵ�A��B��C��DΧ�ɵ��ı���Ϊ�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ʣ����߲��֣��ij���16m������Χ�ɾ���ABCD���������ǣ�������
��ͼ��������ʣ����߲��֣��ij���16m������Χ�ɾ���ABCD���������ǣ�������| A�� | 60m2 | B�� | 63m2 | C�� | 64m2 | D�� | 66m2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com