
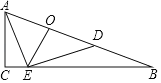
【题目】已知,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在边AB上,以AD为直径的⊙O,与边BC有公共点E,则AD的最小值是_____.
科目:初中数学 来源: 题型:
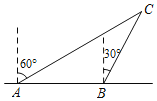
【题目】如图所示,一艘轮船在近海处由西向东航行,点C处有一灯塔,灯塔附近30海里的圆形区域内有暗礁,轮船在A处测得灯塔在北偏东60°方向上,轮船又由A向东航行40海里到B处,测得灯塔在北偏东30°方向上.
(1)求轮船在B处时到灯塔C处的距离是多少?
(2)若轮船继续向东航行,有无触礁危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
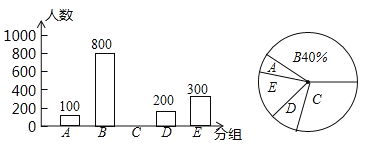
(1)在这次调查中,一共调查了 名市民,扇形统计图中,C组对应的扇形圆心角是 °;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC为⊙O 的弦,OD⊥AB,OD与AC的延长线交于点D,点E在OD上,且∠ECD=∠B.
(1)求证:EC是⊙O的切线;
(2)若OA=3,AC=2,求线段CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
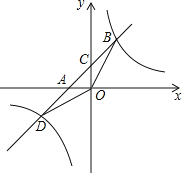
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.
(1)当m=2,a=﹣1时,求b与c的值;
(2)用只含字母a,n的代数式表示b;
(3)当a<0时,函数y=ax2+bx+c满足b2﹣4ac=a,b+c≥2a,n≤﹣![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以BC为直径的⊙O中,点A、E为圆周上两点,过点A作AD⊥BC,垂足为D,作AF⊥CE的延长线于点F,垂足为F,连接AC、AO,已知BD=EF,BC=4.
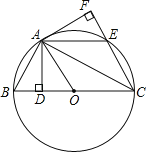
(1)求证:∠ACB=∠ACF;
(2)当∠AEF= °时,四边形AOCE是菱形;
(3)当AC= 时,四边形AOCE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
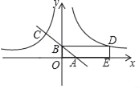
【题目】如图,一次函数y=﹣x+b交x轴于点A,交y轴于点B(0,1),与反比例函数![]() 的图象交于点C,C点的横坐标是﹣2.
的图象交于点C,C点的横坐标是﹣2.
(1)求反比例函数y1的解析式;
(2)设函数![]() 的图象与
的图象与![]() 的图象关于y轴对称,在
的图象关于y轴对称,在![]() 的图象上取一点D(D点的横坐标大于1),过D点作DE⊥x轴于点E,若四边形OBDE的面积为10,求D点的坐标.
的图象上取一点D(D点的横坐标大于1),过D点作DE⊥x轴于点E,若四边形OBDE的面积为10,求D点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com