
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1 , 边B1C1与CD交于点O,则四边形AB1OD的面积是( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣1
﹣1
【答案】D
【解析】方法一:
解:连接AC1 , 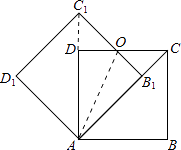
∵四边形AB1C1D1是正方形,
∴∠C1AB1= ![]() ×90°=45°=∠AC1B1 ,
×90°=45°=∠AC1B1 ,
∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1 ,
∴∠B1AB=45°,
∴∠DAB1=90°﹣45°=45°,
∴AC1过D点,即A、D、C1三点共线,
∵正方形ABCD的边长是1,
∴四边形AB1C1D1的边长是1,
在Rt△C1D1A中,由勾股定理得:AC1= ![]() =
= ![]() ,
,
则DC1= ![]() ﹣1,
﹣1,
∵∠AC1B1=45°,∠C1DO=90°,
∴∠C1OD=45°=∠DC1O,
∴DC1=OD= ![]() ﹣1,
﹣1,
∴S△ADO= ![]() ×ODAD=
×ODAD= ![]() ,
,
∴四边形AB1OD的面积是=2× ![]() =
= ![]() ﹣1,
﹣1,
方法二:
解:∵四边形ABCD是正方形,
∴AC= ![]() ,∠OCB1=45°,
,∠OCB1=45°,
∴CB1=OB1
∵AB1=1,
∴CB1=OB1=AC﹣AB1= ![]() ﹣1,
﹣1,
∴S△OB1C= ![]() OB1CB1=
OB1CB1= ![]() (
( ![]() ﹣1)2 ,
﹣1)2 ,
∵S△ADC= ![]() ADAC=
ADAC= ![]() ×1×1=
×1×1= ![]() ,
,
∴S四边形AB1OD=S△ADC﹣S△OB1C= ![]() ﹣
﹣ ![]() (
( ![]() ﹣1)2=
﹣1)2= ![]() ﹣1;
﹣1;
故选:D.
连接AC1 , AO,根据四边形AB1C1D1是正方形,得出∠C1AB1=∠AC1B1=45°,求出∠DAB1=45°,推出A、D、C1三点共线,在Rt△C1D1A中,由勾股定理求出AC1 , 进而求出DC1=OD,根据三角形的面积计算即可.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】菱形ABCD中,对角线AC、BD交于点O,且AC=2BD,以AD为斜边在菱形ABCD同侧作Rt△ADE.
(1)如图1,当点E落在边AB上时.
①求证:∠BDE=∠BAO;
②求 ![]() 的值;
的值;
③当AF=6时,求DF的长.
(2)如图2,当点E落在菱形ABCD内部,且AE=DE时,猜想OE与OB的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= ![]() 在第一象限的图象经过点B.若OA2﹣AB2=12,则k的值为 .
在第一象限的图象经过点B.若OA2﹣AB2=12,则k的值为 . 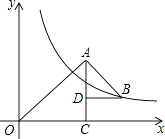
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,ABCD中,BC=8cm,CD=4cm,∠B=60°,点M从点D出发,沿DA方向匀速运动,速度为2cm/s,点N从点B出发,沿BC方向匀速运动,速度为1cm/s,过M作MF⊥CD,垂足为F,延长FM交BA的延长线于点E,连接EN,交AD于点O,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,△AEM≌△DFM?
(2)连接AN,MN,设四边形ANME的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANME的面积是ABCD面积的 ![]() ?若存在,求出相应的t值,若不存在,说明理由;
?若存在,求出相应的t值,若不存在,说明理由;
(4)连接AC,交EN于点P,当EN⊥AD时,求线段OP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为丰富学生的校园生活,准备从某体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买1个足球和2个篮球共需210元.购买2个足球和6个篮球共需580元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需从该体育用品商店一次性购买足球和篮球共100个.要求购买足球和篮球的总费用不超过6000元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F. 
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1.反比例函数y= ![]() 的图象经过A,B两点,则菱形ABCD的面积为( )
的图象经过A,B两点,则菱形ABCD的面积为( ) 
A.2
B.4
C.2 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E. 
(1)求证:DE是⊙O的切线;
(2)若⊙O与AC相切于F,AB=AC=8cm,sinA= ![]() ,求⊙O的半径的长.
,求⊙O的半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进营业额不断增长,某大型超市决定购进甲、乙两种商品,已知甲种商品每件进价为150元,售价为168元;乙种商品每件进价为120元,售价为140元,该超市用42000元购进甲、乙两种商品,销售完后共获利5600元.
(1)该超市购进甲、乙两种商品各多少件?
(2)超市第二次以原价购进甲、乙两种商品共400件,且购进甲种商品的件数多于乙种商品的件数,要使第二次经营活动的获利不少于7580元,共有几种进货方案?写出利润最大的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com