
【题目】已知,如图,ABCD中,BC=8cm,CD=4cm,∠B=60°,点M从点D出发,沿DA方向匀速运动,速度为2cm/s,点N从点B出发,沿BC方向匀速运动,速度为1cm/s,过M作MF⊥CD,垂足为F,延长FM交BA的延长线于点E,连接EN,交AD于点O,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,△AEM≌△DFM?
(2)连接AN,MN,设四边形ANME的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANME的面积是ABCD面积的 ![]() ?若存在,求出相应的t值,若不存在,说明理由;
?若存在,求出相应的t值,若不存在,说明理由;
(4)连接AC,交EN于点P,当EN⊥AD时,求线段OP的长度.
【答案】
(1)
解:∵四边形ABCD为平行四边形,
∴AD=BC=8.
∵△AEM≌△DFM,
∴AM=MD=4.
∴2t=4.
∴t=2
(2)
解:如图1所示:过点A作AG⊥BC,垂足为G.
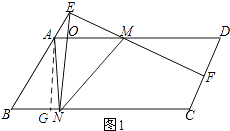
∵∠AGB=90°,∠A=60°,
∴AG= ![]() AB=2
AB=2 ![]()
∵MD=2t,
∴AM=8﹣2t.
∵AB∥CD,MF⊥CD,
∴MF⊥AB.
∴∠MEA=90°.
∵AD∥BC,
∴∠EAM=∠B=60°.
∴AE= ![]() AM=4﹣t,ME=
AM=4﹣t,ME= ![]() (4﹣t).
(4﹣t).
∴y=S△ANM+S△AEM= ![]() ×(8﹣2t)×2
×(8﹣2t)×2 ![]() +
+ ![]() ×(4﹣t)×
×(4﹣t)× ![]() ×(4﹣t)=
×(4﹣t)= ![]() t2﹣6
t2﹣6 ![]() t+16
t+16 ![]() .
.
∴y= ![]() t2﹣6
t2﹣6 ![]() t+16
t+16 ![]()
(3)
解:设运动时间t秒时,四边形ANME的面积是ABCD面积的 ![]() .
.
根据题意得: ![]() t2﹣6
t2﹣6 ![]() t+16
t+16 ![]() =
= ![]() ×8×2
×8×2 ![]() .
.
整理得:t2﹣12t+11=0.
解得t=1或t=11(舍去).
所以当t=1时,四边形ANME的面积是ABCD面积的 ![]()
(4)
解:如图2所示:过A作AG⊥BC,垂足为G.
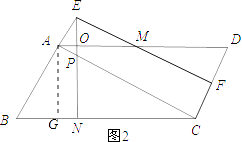
∵由(2)可知AE=4﹣t.
∴BE=AB+AE=8﹣t.
∵∠B=60°,EN⊥BC,AG⊥BC,
p>∴BN=又∵BN=t,
∴4﹣ ![]() t=t.
t=t.
解得:t= ![]() .
.
∴GN=BN﹣BG= ![]() .
.
∴AO= ![]() ,NC=
,NC= ![]() .
.
设PO=x,则PN=2 ![]() ﹣x.
﹣x.
∵AO∥NC,
∴△AOP∽△CNP.
∴ ![]() ,即
,即 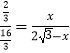 .
.
解得:x= ![]() .
.
∴OP的长为 ![]()
【解析】(1)由全等三角形的性质可知AM=MD=4,故此得到2t=4,于是可求得t的值;(2)过点A作AG⊥BC,垂足为G.在Rt△ABG中依据特殊锐角三角函数值可求得AG的长,由题意可得到AM=8﹣2t,然后再△AEM中依据特殊锐角三角函数值可求得AE、ME的长,最后依据y=S△ANM+S△AEM可得到y与x的函数关系式;(3)设运动时间t秒时,四边形ANME的面积是ABCD面积的 ![]() ,根据题意列方程求解即可;(4)过A作AG⊥BC,垂足为G.由(2)可知AE=4﹣t,从而得到BE的长,然后在△AGB和△BNE中,依据特殊锐角三角函数值可求得NB的长(含t的式子),接下来依据BN=t列出关于t的方程,从而可求得t的值,于是可求得AO、NC的长,最后证明△AOP∽△CNP,最后依据相似三角形的性质可求得OP的长.
,根据题意列方程求解即可;(4)过A作AG⊥BC,垂足为G.由(2)可知AE=4﹣t,从而得到BE的长,然后在△AGB和△BNE中,依据特殊锐角三角函数值可求得NB的长(含t的式子),接下来依据BN=t列出关于t的方程,从而可求得t的值,于是可求得AO、NC的长,最后证明△AOP∽△CNP,最后依据相似三角形的性质可求得OP的长.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα= ![]() .
. 
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55cm,求铁环钩MF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点,正方形边长的整点称为边整点,如图,第一个正方形有4个边整点,第二个正方形有8个边整点,第三个正方形有12个边整点,…,按此规律继续作下去,若从内向外共作了5个这样的正方形,那么其边整点的个数共有个,这些边整点落在函数y= ![]() 的图象上的概率是 .
的图象上的概率是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y= ![]() ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,连接AB,BC.
,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,连接AB,BC. 
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,在△ABC中,AD是中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF. 
(2)如图2,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,求AD的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1 , 边B1C1与CD交于点O,则四边形AB1OD的面积是( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课题研究小组对本校九年级全体同学体育测试情况进行调查,他们随即抽查部分同学体育测试成绩(由高到低分A、B、C、D四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该课题研究小组共抽查了名同学的体育测试成绩,扇形统计图中B级所占的百分比b= , D级所在小扇形的圆心角的大小为;
(2)请直接补全条形统计图;
(3)若该校九年级共有600名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红、小兵玩捉迷藏游戏,小红、小兵可以在A,B,C三个地点中任意一处藏身,小明去寻找他们.
(1)求小明在B处找到小红的概率;
(2)求小明在同一地点找到小红和小兵的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com