
【题目】学校6名教师和234名学生集体外出活动,准备租用45座大车或30座小车.若租用1辆大车2辆小车共需租车费1000元;若租用2辆大车一辆小车共需租车费1100元.
(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名教师,且总租车费用不超过2300元,求最省钱的租车方案.
【答案】(1)大车每辆的租车费是400元、小车每辆的租车费是300元;(2)最省钱的租车方案是:4辆大车,2辆小车
【解析】
(1)设大车每辆的租车费是x元、小车每辆的租车费是y元.根据题意:“租用1辆大车2辆小车共需租车费1000元”;“租用2辆大车一辆小车共需租车费1100元”;列出方程组,求解即可;
(2)根据汽车总数不能小于![]() (取整为6)辆,即可求出共需租汽车的辆数;设租用大车m辆,则租车费用Q(单位:元)是m的函数,由题意得出400m+300(6-m)≤2300,得出取值范围,分析得出即可.
(取整为6)辆,即可求出共需租汽车的辆数;设租用大车m辆,则租车费用Q(单位:元)是m的函数,由题意得出400m+300(6-m)≤2300,得出取值范围,分析得出即可.
解:(1)设大车每辆的租车费是x元、小车每辆的租车费是y元.
可得方程组![]() ,
,
解得![]() .
.
答:大车每辆的租车费是400元、小车每辆的租车费是300元;
(2)由每辆汽车上至少要有1名老师,汽车总数不能大于6辆;
又要保证240名师生有车坐,汽车总数不能小于![]() (取整为6)辆,
(取整为6)辆,
综合起来可知汽车总数为6辆.
设租用m辆大型车,则租车费用Q(单位:元)是m的函数,
即Q=400m+300(6-m);
化简为:Q=100m+1800,
依题意有:100m+1800≤2300,
∴m≤5,
又要保证240名师生有车坐,45m+30(6-m)≥240,解得m≥4,
所以有两种租车方案,
方案一:4辆大车,2辆小车;
方案二:5辆大车,1辆小车.
∵Q随m增加而增加,
∴当m=4时,Q最少为2200元.
故最省钱的租车方案是:4辆大车,2辆小车.


科目:初中数学 来源: 题型:
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.

(1)填空:A,B两地相距 千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
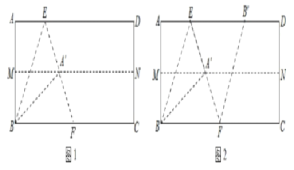
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
(1)证明:∠ABE=30°;
(2)证明:四边形BFB′E为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC与△A'B'C在平面直角坐标系中的位置如图.

(1)分别写出B、B'的坐标:B______;B′______;
(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为______;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
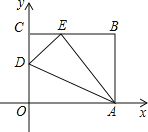
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市进行“新城区改造建设”,有甲、乙两种车参加运土,已知5辆甲种车和2辆乙种车一次共可运土64米![]() ,3辆甲种车和1辆乙种车一次共可运土36米
,3辆甲种车和1辆乙种车一次共可运土36米![]() .
.
(1)求甲、乙两种车每辆一次可分别运土多少米![]() ;
;
(2)某公司派甲、乙两种汽车共10辆参加运土,且一次运土总量不低于100米![]() ,求公司最多要派多少辆甲种汽车参加运土.
,求公司最多要派多少辆甲种汽车参加运土.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(![]() )天的售价与销量的相关信息如下表:
)天的售价与销量的相关信息如下表:
时间(天) |
|
|
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | 200-2x |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
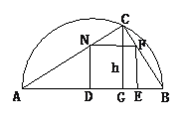
【题目】在直径为AB的半圆内,划出一块三角形区域,如图所示,使三角形的一边为AB,顶点C在半圆圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形水池DEFN,其中D、E在AB上,如图24-94的设计方案是使AC=8,BC=6.
(1)求△ABC的边AB上的高h.
(2)设DN=x,且![]() ,当x取何值时,水池DEFN的面积最大?
,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为了保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开大树.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com