
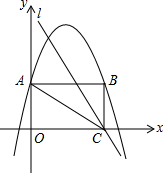
 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�Ǿ��Σ���A��C�ֱ���y�ᡢx���ϣ���B�ڵ�һ���ޣ�������y=-$\frac{1}{2}{x}^{2}$+4x+6����A��B���㣮
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�Ǿ��Σ���A��C�ֱ���y�ᡢx���ϣ���B�ڵ�һ���ޣ�������y=-$\frac{1}{2}{x}^{2}$+4x+6����A��B���㣮���� ��1�����������߽���ʽ��õ�A�����꣬Ȼ���Ͼ��ε����ʺ������ߵ����ʿ�����õ�B��C�����ꣻ
��2�����ݶԳ��Ժ��ɶ���������õ�E�����꣬�Ӷ��������ֱ��l�Ľ���ʽ��
��3����ȷ������O����ֱ��l�ĶԳƵ�E�����꣬�������ֱ��EF����ʽ�����ɵó�ֱ��EF�������ߵĽ�����ǵ�P��
��� �⣺��1����y=-$\frac{1}{2}$x2+4x+6��
�൱x=0ʱ��y=6��
��A��0��6����
��y=-$\frac{1}{2}$x2+4x+6=-$\frac{1}{2}$��x-4��2+14��
��������ߵĶԳ�����x=4��
���A��B����ֱ��x=4�Գƣ�
��B��8��6����
��C��8��0����
��2������ͼ��ʾ��
����֪�ɵã�DE=BE��CD=CB��
��A��0��6����B��8��6������C��8��0����
��BC=6��OC=8��
��AC=10��CD=6��
��AD=4��
��AE=a��
��EB=8-a��
��DE=8-a��
��42+��8-a��2=a2��
��ã�a=5��
���E��������5��6��
�����C��8��0������E��5��6����ֱ��l�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{5k+b=6}\\{8k+b=0}\end{array}\right.$����$\left\{\begin{array}{l}{k=-2}\\{b=16}\end{array}\right.$��
��ֱ��l�Ľ���ʽΪ��y=-2x+16��
��3����ͼ1��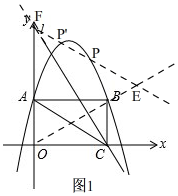 �ɣ�2��֪��ֱ��l�Ľ���ʽΪy=-2x+16��
�ɣ�2��֪��ֱ��l�Ľ���ʽΪy=-2x+16��
������O����ֱ��l�ĶԳƵ�E��$\frac{64}{5}$��$\frac{32}{5}$����
ֱ��l��y��Ľ���ΪF��0��16����
��OF=EF��ֱ��EF�Ľ���ʽΪy=-$\frac{3}{4}$x+16�٣�
�ߵ�P��������y=-$\frac{1}{2}{x}^{2}$+4x+6���ϣ�
�����٢ڵã�x=$\frac{19��\sqrt{41}}{4}$��
��P��$\frac{19+\sqrt{41}}{4}$��$\frac{199-3\sqrt{41}}{16}$����$\frac{19-\sqrt{41}}{4}$��$\frac{199+3\sqrt{41}}{16}$��
���� �����Ƕ��κ������ۺ��⣬��Ҫ��������������x��Ľ������꣬�۵������ʣ���ƽ���߶�������ֱƽ���ߵ����ʣ��⣨2���Ĺؼ������ý�ƽ���ߵ����ʽ������̣��⣨3���Ĺؼ��жϳ���P��ֱ��EF�������ߵĽ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�������ص���ֱ�������Σ�������һ��ֱ������������BC����ƽ��BE�ij��Ⱦ͵õ���ͼ�Σ�����Ӱ���ֵ��������λ�����ף�
��ͼ�������ص���ֱ�������Σ�������һ��ֱ������������BC����ƽ��BE�ij��Ⱦ͵õ���ͼ�Σ�����Ӱ���ֵ��������λ�����ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij��������������A��B��C��ͬһ��·�ϣ��ף��������οʹӾ���A�������ײ��е�����C���ҳ˾����۹�ȵ�����B����B��ͣ��һ��ʱ����ٲ��е�����C���ף��������뿪����A���·��S���ף�����ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ��������Ϣ�ش��������⣺
ij��������������A��B��C��ͬһ��·�ϣ��ף��������οʹӾ���A�������ײ��е�����C���ҳ˾����۹�ȵ�����B����B��ͣ��һ��ʱ����ٲ��е�����C���ף��������뿪����A���·��S���ף�����ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ��������Ϣ�ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��AOE=��COD��������OCƽ�֡�BOE����EOD=30�㣬���AOD�Ķ�����
��ͼ����֪��AOE=��COD��������OCƽ�֡�BOE����EOD=30�㣬���AOD�Ķ������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com