
 某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题:
某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题:分析 (1)观察图象即可解决问题.
(2)利用待定系数法求一次函数解析式进而利用两函数相等时即为相遇时,求出时间即可;
(3)根据题意得出要使两人相距400米,乙需要步行的距离为:5400-3000-400=2000(米),乙所用的时间为:30分钟,进而得出答案.
解答 解:(1)由图象可知,景点C距离A5400千米,景点B距离景点A3000千米,甲的速度为$\frac{5400}{90}$=60米/分钟,
故答案为5400,3000,60米/分钟.
(2)设S甲=kt,将(90,5400)代入得:
5400=90k,
解得:k=60,
∴S甲=60t;
当0≤t≤30,设S乙=at+b,将(20,0),(30,3000)代入得出:
$\left\{\begin{array}{l}{20a+b=0}\\{30a+b=3000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=300}\\{b=-6000}\end{array}\right.$,
∴当20≤t≤30,S乙=300t-6000.
当S甲=S乙,
∴60t=300t-6000,
解得:t=25,
∴乙出发后5分钟与甲第一次相遇.
(3)由题意可得出;当甲到达C地,乙距离C地400米时,
乙需要步行的距离为:5400-3000-400=2000(米),乙所用的时间为:90-60=30(分钟),
故乙从景点B步行到景点C的速度至少为:$\frac{2000}{30}$≈66.7(米/分),
答:乙从景点B步行到景点C的速度至少为66.7米/分.
点评 此题主要考查了待定系数法求一次函数解析式、行程问题等知识,解题关键是理解题意,读懂图象信息,学会构建一次函数解决实际问题,属于中考常考题型.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
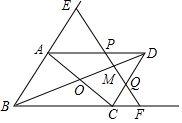 如图,已知?ABCD的对角线交于O点,M为OD的中点,过M的直线分别交AD、CD于P、Q.交BA、BC的延长线于E、F.求证:PE+QF=2PQ.
如图,已知?ABCD的对角线交于O点,M为OD的中点,过M的直线分别交AD、CD于P、Q.交BA、BC的延长线于E、F.求证:PE+QF=2PQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
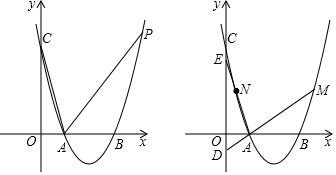
 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C分别在y轴、x轴上,点B在第一象限,抛物线y=-$\frac{1}{2}{x}^{2}$+4x+6经过A、B两点.
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C分别在y轴、x轴上,点B在第一象限,抛物线y=-$\frac{1}{2}{x}^{2}$+4x+6经过A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
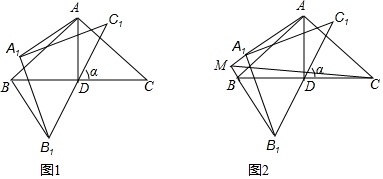
 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com