练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】证明一个四边形是正方形，使用次数最少的方法对折，则应该对折（　　）

    A.1次B.2次C.3次D.4次

    【答案】B

    【解析】

    先对折一次得到2组邻角相等，且一组对边相等，再对折一次得到对角相等，两组邻边长度相等，即可证得正方形 .

    把四边形对折1次（共2层），2组邻角相等，且一组对边相等；

    将四边形展开后沿对角线对折，则对角相等，两组邻边长度相等，所以4个角相等，且4条边相等．则这个四边形是正方形．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】旅行社组织了甲、乙两个旅游团到游乐场游玩，两团总报名人数为120人，其中甲团人数不超过50人，游乐场规定一次性购票50人以上可享受团队票．门票价格如下：

    旅行社经过计算后发现，如果甲、乙两团合并成一个团队购票可以比分开购票节约300元．

    （1）求甲、乙两团的报名人数；

    （2）当天到达游乐场后发现团队票价格作了临时调整，团队票A每张降价a元，团队票B每张降价2a元，同时乙团队因故缺席了30人，此时甲、乙两团合并成一个团队购票可以比分开购票节约225元，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AD= AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：
    ①∠AED=∠CED；
    ②OE=OD；
    ③BH=HF；
    ④BC﹣CF=2HE；
    ⑤AB=HF．
    其中正确的有（ ）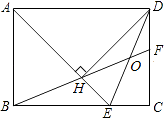

    A.①②③④⑤
    B.①②③④
    C.①③④⑤
    D.①②③⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE．

    （1）求证：DE是⊙O的切线；

    （2）若AE=6，∠D=30°，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】知识的迁移与应用

    问题一：甲、乙两车分别从相距180km的 A、B两地出发，甲车速度为36 km/h，乙车速度为24km/h，两车同时出发，相向而行，　　 后两车相距120 km？

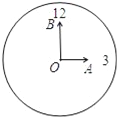
    问题二：将线段弯曲后可视作钟表的一部分，如图，在一个圆形时钟的表面上，OA表示时针，OB表示分针（O为两针的旋转中心）．下午3点时，OA与OB成直角．

    （1）3:40时，时针与分针所成的角度　　；

    （2）分针每分钟转过的角度为　　，时针每分钟转过的角度为　　；

    （3）在下午3点至4点之间，从下午3点开始，经过多少分钟，时针与分针成60°角？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD的对角线AC与BD交于点O，AC=6，BD=8．动点E从点B出发，沿着B﹣A﹣D在菱形ABCD的边上运动，运动到点D停止．点F是点E关于BD的对称点，EF交BD于点P，若BP=x，△OEF的面积为y，则y与x之间的函数图象大致为（　　）

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形，且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍，我们把这条对角线叫做这个四边形的黄金线，这个四边形叫做黄金四边形．

    （1）如图1，在四边形ABCD中，AB=AD=DC，对角线AC，BD都是黄金线，且AB＜AC，CD＜BD，求四边形ABCD各个内角的度数；

    （2）如图2，点B是弧AC的中点，请在⊙O上找出所有的点D，使四边形ABCD的对角线AC是黄金线（要求：保留作图痕迹）；

    （3）在黄金四边形ABCD中，AB=BC=CD，∠BAC=30°，求∠BAD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正方形ABOD的周长为4，点P到x轴、y轴的距离与点A到x轴、y轴的距离分别相等．

    (1)请你写出正方形ABOD各顶点的坐标；

    (2)求点P的坐标及三角形PDO的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程2x2+4x+k-1=0有实数根，k为正整数.

    （1）求k的值；

    （2）当此方程有两个非零的整数根时，将关于x的二次函数y=2x2+4x+k-1的图象向下平移8个单位，求平移后的图象的解析式；

    (3) 在（2）的条件下，将平移后的二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象.请你结合这个新的图像回答：当直线y=0.5x+b (b<k)与此图象有两个公共点时，b的取值范围.

    查看答案和解析>>

    同步练习册答案