
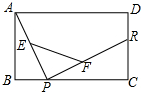
 如图,矩形ABCD中,AD=13,DC=10,P是BC上的一点,R、E、F分别是DC、AP、RP的中点,当点P在BC上由B向C移动时,那么EF的长度$\frac{\sqrt{194}}{2}$.
如图,矩形ABCD中,AD=13,DC=10,P是BC上的一点,R、E、F分别是DC、AP、RP的中点,当点P在BC上由B向C移动时,那么EF的长度$\frac{\sqrt{194}}{2}$. 分析 连接AR.在Rt△ADR中,利用勾股定理求出AR,再利用三角形的中位线定理即可求出EF.
解答 解:如图,连接AR.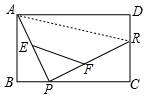
∵四边形ABCD是矩形,
∴∠D=90°,
∵DR=RC=5,AD=13,
∴AR=$\sqrt{A{D}^{2}+D{R}^{2}}$=$\sqrt{1{3}^{2}+{5}^{2}}$=$\sqrt{194}$,
∵AE=EP,PF=FR,
∴EF=$\frac{1}{2}$AR=$\frac{\sqrt{194}}{2}$,
故答案为$\frac{\sqrt{194}}{2}$.
点评 本题考查矩形的性质、勾股定理、三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:选择题
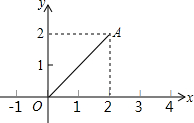 如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )| A. | (4,0) | B. | (-2$\sqrt{2}$,0) | C. | (1,0) | D. | (2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
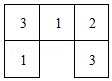 如图是一些小正方块所搭几何体从上面看到的形状图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体从正面和左面看到的形状图:(要求用直尺或三角板画图)
如图是一些小正方块所搭几何体从上面看到的形状图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体从正面和左面看到的形状图:(要求用直尺或三角板画图)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
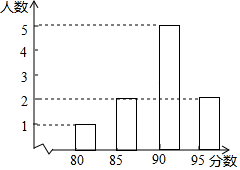 如图,对参加数学竞赛的10名学生的测试成绩进行了统计,对于这10名学生的测试成绩,下列说法错误的是( )
如图,对参加数学竞赛的10名学生的测试成绩进行了统计,对于这10名学生的测试成绩,下列说法错误的是( )| A. | 众数是90 | B. | 中位数是90 | C. | 平均数是90 | D. | 极差是15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
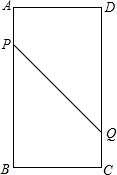 如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.
如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com