
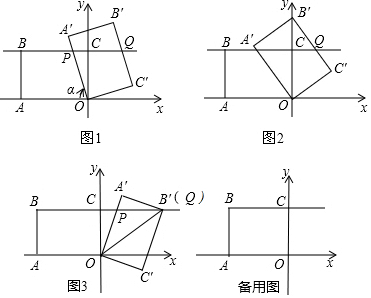
���� ��1��������һ������ֱ�ǵ�ƽ���ı��ν����жϵ���=90��ʱ�����dz�����ıȣ�
��2���������������������CP�ıȣ��Ϳ����BP��PQ��ֵ��
�ڸ��ݹ��ɶ������PB��ij����ٸ��������ε������ʽ���м��㣮
��3������ȫ�������κ�ֱ�������Σ����ù��ɶ������PC�ij�����һ���������
��� 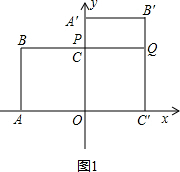 �⣺��1��ͼ1���ı���OA��B��C�����״�Ǿ��Σ�
�⣺��1��ͼ1���ı���OA��B��C�����״�Ǿ��Σ�
�ߵ�A������Ϊ��-8��0������B��-8��6����
��AB��OC��
��BC��x�ᣬ
���ı���OABC��ƽ���ı��Σ�
��OC��OA��
��ƽ���ı���OABC����״�Ǿ��Σ�
����=90��ʱ��P��C�غϣ���ͼ1��
BP=8��BQ=BP+OC=8+6=14��
��$\frac{BP}{PQ}=\frac{4}{3}$��
���Ǿ��εij�����ıȣ���$\frac{BP}{BQ}=\frac{4}{7}$��
�ʴ�Ϊ���Σ�$\frac{4}{7}$��
��2����ͼ2���ߡ�POC=��B��OA�䣬��PCO=��OA��B��=90�㣬
���COP�ס�A��OB�䣮
��$\frac{CP}{A'B'}=\frac{OC}{OA'}$����$\frac{CP}{6}=\frac{6}{8}$��
��CP=$\frac{9}{2}$��BP=BC-CP=$\frac{7}{2}$��
ͬ����B��CQ�ס�B��C��O��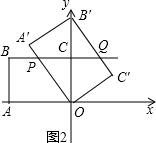
��$\frac{CQ}{C'O}=\frac{B'C}{B'C'}$��
��$\frac{CQ}{6}=\frac{10-6}{8}$
��CQ=3��BQ=BC+CQ=11��
��$\frac{BP}{PQ}=\frac{\frac{7}{2}}{\frac{9}{2}+3}=\frac{7}{15}$��
��$\frac{BP}{BQ}=\frac{7}{22}$��
��ͼ3���ڡ�OCP�͡�B��A��P�У�$\left\{\begin{array}{l}{��OPC=��B'PA'}\\{��OCP=��A'=90��}\\{OC=B'A'}\end{array}\right.$��
���OCP�ա�B��A��P��AAS����
��OP=B��P��
��B��P=x��
��Rt��OCP����8-x��2+62=x2��
���x=$\frac{25}{4}$��
��S��OPB��=$\frac{1}{2}$��$\frac{25}{4}$��6=$\frac{75}{4}$��
��3�����������ĵ�P�͵�Q��ʹBP=$\frac{1}{2}$BQ��
��P��������P1��-9-$\frac{3\sqrt{6}}{2}$��6����P2��-$\frac{7}{4}$��6����
���ɣ�
����Q��QH��OA����H������OQ����QH=OC��=OC��
��S��POQ=$\frac{1}{2}$PQ•OC��S��POQ=$\frac{1}{2}$OP•QH��
��PQ=OP��
��BP=x��
��BP=$\frac{1}{2}$BQ��
��BQ=2x��
��ͼ4��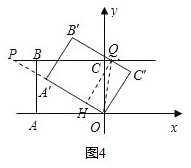 ����P�ڵ�B���ʱ��
����P�ڵ�B���ʱ��
OP=PQ=BQ+BP=3x��
��Rt��PCO����8+x��2+62=��3x��2��
���x1=1+$\frac{3\sqrt{6}}{2}$��x2=1-$\frac{3\sqrt{6}}{2}$������ʵ�ʣ���ȥ����
��PC=BC+BP=9+$\frac{3\sqrt{6}}{2}$��
��P��-9-$\frac{3\sqrt{6}}{2}$��6����
��ͼ5��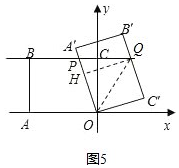 ����P�ڵ�B�Ҳ�ʱ��
����P�ڵ�B�Ҳ�ʱ��
��OP=PQ=BQ-BP=x��PC=8-x��
��Rt��PCO����8-x��2+62=x2�����x=$\frac{25}{4}$��
��PC=BC-BP=8-$\frac{25}{4}$=$\frac{7}{4}$��
��P��-$\frac{7}{4}$��6����
���Ͽ�֪�����ڵ�P��-9-$\frac{3\sqrt{6}}{2}$��6����-$\frac{7}{4}$��6����ʹBP=$\frac{1}{2}$BQ��
���� ���⿼������ת�����ʣ����ε����ʣ�ȫ�������ε��ж������ʣ����������ε��ж������ʣ����ɶ������ر�ע������ת�Ĺ����еĶ�Ӧ�߶���ȣ��ܹ���һ��δ֪����ʾͬһ��ֱ�������ε�δ֪�ߣ��Ȿ��Ĺؼ��Ǹ��ݹ��ɶ����з�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���ACB=90�㣬BEƽ�֡�ABC��DE��AB��D��AE=3ED�����AC=12cm����ôDE�ij�Ϊ3cm��
��ͼ���ڡ�ABC�У���ACB=90�㣬BEƽ�֡�ABC��DE��AB��D��AE=3ED�����AC=12cm����ôDE�ij�Ϊ3cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��3��4 | B�� | 4��5��6 | C�� | 1��$\sqrt{2}$��$\sqrt{3}$ | D�� | 2��$\sqrt{2}$��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
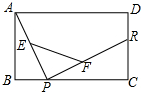 ��ͼ������ABCD�У�AD=13��DC=10��P��BC�ϵ�һ�㣬R��E��F�ֱ���DC��AP��RP���е㣬����P��BC����B��C�ƶ�ʱ����ôEF�ij���$\frac{\sqrt{194}}{2}$��
��ͼ������ABCD�У�AD=13��DC=10��P��BC�ϵ�һ�㣬R��E��F�ֱ���DC��AP��RP���е㣬����P��BC����B��C�ƶ�ʱ����ôEF�ij���$\frac{\sqrt{194}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �������
��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
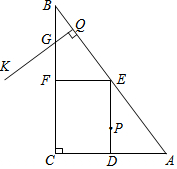 ��ͼ����Rt��ABC�У���C=90�㣬AB=50��AC=30��D��E��F�ֱ���AC��AB��BC���е㣮��P�ӵ�D����������DE-EF-FC-CD��ÿ��7����λ�����ٶ������˶�����Q�ӵ�B������BA������ÿ��4����λ�����ٶ������˶�������Q������QK��AB��������BC-CA�ڵ�G����P��Qͬʱ����������P����һ�ܻص���Dʱֹͣ�˶�����QҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0����
��ͼ����Rt��ABC�У���C=90�㣬AB=50��AC=30��D��E��F�ֱ���AC��AB��BC���е㣮��P�ӵ�D����������DE-EF-FC-CD��ÿ��7����λ�����ٶ������˶�����Q�ӵ�B������BA������ÿ��4����λ�����ٶ������˶�������Q������QK��AB��������BC-CA�ڵ�G����P��Qͬʱ����������P����һ�ܻص���Dʱֹͣ�˶�����QҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
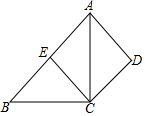 ��ͼ���ڡ�ABC�У���ACB=90�㣬E��AB���е㣬AD��EC��CD��AB�����ж��ı���ADCE����״����֤����Ľ��ۣ�
��ͼ���ڡ�ABC�У���ACB=90�㣬E��AB���е㣬AD��EC��CD��AB�����ж��ı���ADCE����״����֤����Ľ��ۣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com