
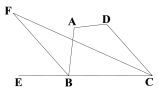
����Ŀ����Rt��ABC����C=90�㣬DΪAB����һ�㣬��M��N�ֱ���BC��AC���ϣ���DM��DN����MF��AB�ڵ�F��NE��AB�ڵ�E��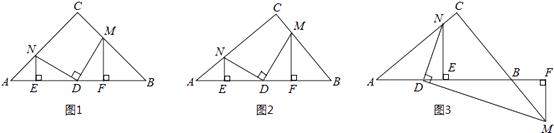
��1��������֤����ͼ1����AC=BC����DΪAB�е㣬��֤��DM=DN��AE=DF��
��2����չ̽������AC��BC��
����ͼ2����DΪAB�е㣬��1���е�����������һ���Գ�������ָ��������֤����
����ͼ3����BD=kAD�������С���M��BC���ϡ���Ϊ����M���߶�CB���ӳ����ϡ��������������䣬��̽��AE��DF��������ϵ������֤����
���𰸡�
��1��֤������AC=BC�����ABCΪ����ֱ�������Σ�

���ͼ1��ʾ������CD����CD��AB���֡�DM��DN�����1=��2��
�ڡ�AND���CMD�У� 
���AND�ա�CMD��ASA����
��DN=DM��
�ߡ�4+��1=90�㣬��1+��3=90�㣬���4=��3��
�ߡ�1+��3=90�㣬��3+��5=90�㣬���1=��5��
�ڡ�NED���DFM�У� 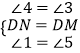
���NED�ա�DFM��ASA����
��NE=DF��
�ߡ�ANEΪ����ֱ�������Σ���AE=NE����AE=DF
��2���ٴ�AE=DF��
֤��һ���ɣ�1��֤����֪����DEN�ס�MFD
�� ![]() ����MFEN=DEDF��
����MFEN=DEDF��
ͬ����AEN�ס�MFB��
�� ![]() ����MFEN=AEBF��
����MFEN=AEBF��
��DEDF=AEBF��
�ࣨAD��AE��DF=AE��BD��DF����
��ADDF=AEBD����AE=DF��
֤���������ͼ2��ʾ������D��DP��BC�ڵ�P��DQ��AC�ڵ�Q��
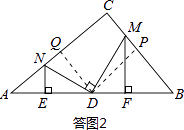
��DΪAB�е㣬
��DQ=PC=PB��
��֤��DMF�ס�NDE���� ![]() ��
��
��֤��DMP�ס�DNQ���� ![]() ��
��
�� ![]() ��
��
��֤��AEN�ס�DPB���� ![]() ��
��
�� ![]() ����AE=DF��
����AE=DF��
�ڴ�DF=kAE��
֤��һ���ɢ�ͬ���ɵã�DEDF=AEBF��
�ࣨAE��AD��DF=AE��DF��BD��
��ADDF=AEBD
��BD=kAD
��DF=kAE��
֤���������ͼ3������D��DP��BC�ڵ�P��DQ��AC�ڵ�Q��
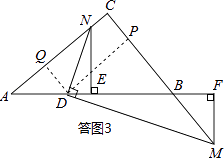
��֤��AQD�ס�DPB���� ![]() ����PB=kDQ��
����PB=kDQ��
�ɢ�ͬ���ɵã� ![]() ��
��
�� ![]() ��
��
�֡� ![]() ��
��
�� ![]() ��
��
��DF=kAE
����������1������CD������֤����AND�ա�CMD������ȫ�������ε����ʿɵõ�DN=DM��Ȼ����֤����NED�ա�DFM���Ӷ��ɵõ�DF=NE��Ȼ�����ݵ��������ε����ʿɵõ�AE=NE=DF��
��2������DΪAB�е㣬���DEN�ס�MFD����AEN�ס�MFB��Ȼ���������������ε������г�����ʽ�������������߶α�����ϵ����֤��AE=DF������Ȼ����������BD=kAD��֤��˼·�������.
�����㾫�����������⣬������Ҫ�˽����������ε��ж�������(���������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��)��


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD���ڽǡ�DCB����ǡ�ABE��ƽ�����ཻ�ڵ�F.
��1����BF��CD����ABC=80�㣬���DCB�Ķ�����
��2����֪�ı���ABCD�У���A=105����D=125�����F�Ķ�����
��3�������F����A����D֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���辩����ɫ���ȣ�����������ˮ�ʣ�ij���۹�˾��������10̨��ˮ�����豸������A��B�����ͺŵ��豸������ÿ̨�ļ۸����´�����ˮ�����±���

�����飺����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
��1����x��y��ֵ��
��2��������۹�˾������ˮ�����豸���ʽ���105��Ԫ��������۹�˾���ļ��ֹ�����
��3���ڣ�2���������£�����´�����ˮ��������2040�֣�Ϊ�˽�Լ�ʽ���Ϊ�ù�˾���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С���ֱ�Ӽغ��ҵ�ͬʱ��������ͬһ��·������У�С����ʼ�ܲ�����;��Ϊ���У������ҵ�ǡ����![]() С�������г���
С�������г���![]() ���ٶ�ֱ�ӵ��أ�������ص�·��
���ٶ�ֱ�ӵ��أ�������ص�·��![]() ������뿪�����ص�ʱ��
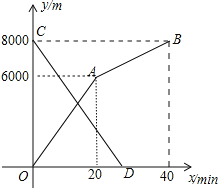
������뿪�����ص�ʱ��![]() ֮��ĺ���ͼ����ͼ��ʾ��
֮��ĺ���ͼ����ͼ��ʾ��
![]() �ס�������֮���·��Ϊ______m��С�����е��ٶ�Ϊ______
�ס�������֮���·��Ϊ______m��С�����е��ٶ�Ϊ______![]() ��
��
![]() ��С����ص�·��y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��С����ص�·��y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
![]() ������������ʱ�䣮
������������ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽�ѧ�������š����������������֡�Ϸ��������ӽ�Ŀ��ϲ������������������������ѧ�������ݵ������ݽ������������������µIJ�����ͳ��ͼ��
����������ϵ���Ϣ���ش��������⣺
��1�����ι���������ѧ����������ϲ��Ϸ�������ˣ�������ͳ��ͼ�У���ϲ�������Ķ�Ӧ���ε�Բ�ĽǴ�С�� ��
��2����������ͳ�Ʒ��������Ƹ�У2000��ѧ������ϲ�����ŵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
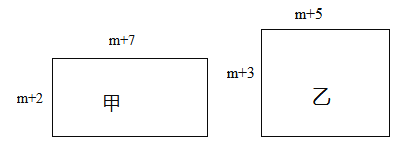
����Ŀ����֪�мס������������Σ����ǵı߳���ͼ��ʾ��mΪ��������������ֱ�ΪS1��S2��
��1����Ƚ�S1��S2�Ĵ�С�� S1�� ��S2��
��2����һ������������ܳ���ȣ�
����������εı߳����ú�m�Ĵ���ʽ��ʾ����
�����������ε����ΪS3����̽����S3��S1�IJ��S3��S1���Ƿ�Ϊ��������Ϊ������������������������ǣ���˵�����ɣ�
��3������������0��n��|S1��S2|������n����ֻ��8����ֱ��д��m��ֵ���ֱ����S1��S2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����һ��ͼ���е�ĸ��������е�1��ͼ�й���4���㣬��2��ͼ�й���10���㣬��3��ͼ�й���19���㣬�������˹��ɵ�100��ͼ�й��е�ĸ�����
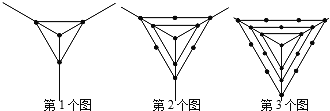
A. 15151B. 15152C. 15153D. 15154
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
=y2+8y+16 ���ڶ�����
=��y+4��2����������
=��x2��4x+4��2�����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ |
B��ƽ���ʽ |
C�������͵���ȫƽ����ʽ |
D�����������ȫƽ����ʽ |
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________�����������������������������������ף���ֱ��д����ʽ�ֽ�������_________ ��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=m ��x��1���� x��4����ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�������ΪC�����ö��κ�����ͼ�����x�ᷭ�ۣ�����ͼ��Ķ���ΪD�����ı���ACBDΪ�����Σ���m��ֵΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com