
 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗? 分析 作DH⊥AB于H,根据正弦、余弦的定义求出DE、CE,根据正切的概念求出AH,计算即可.
解答 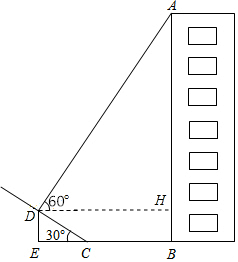 解:作DH⊥AB于H,
解:作DH⊥AB于H,
在Rt△CDE中,DE=$\frac{1}{2}$CD=3,CE=$\frac{\sqrt{3}}{2}$CD=3$\sqrt{3}$,
∴BE=3$\sqrt{3}$+8,
在Rt△ADH中,AH=DH•tan∠ADH=9+8$\sqrt{3}$,
∴AB=AH+BH=12+8$\sqrt{3}$,
答:楼房AB的高度为(12+8$\sqrt{3}$)米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题、仰角俯角问题,掌握坡度坡角、仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:选择题
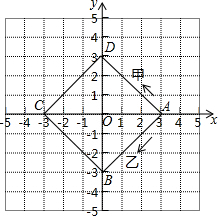 如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )
如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )| A. | (3,0) | B. | (-1,2) | C. | (-3,0) | D. | (-1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y=x-2与反比例函数y=$\frac{3}{x}$的图象交于A、B两点.
如图,已知一次函数y=x-2与反比例函数y=$\frac{3}{x}$的图象交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
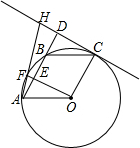 如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
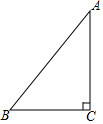 如图,已知Rt△ABC,∠C=90°,AC≠BC.
如图,已知Rt△ABC,∠C=90°,AC≠BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
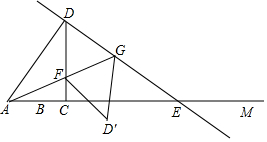 如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.
如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com