
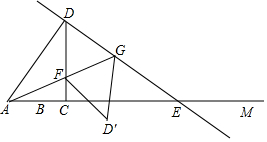
 如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.
如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.分析 (1)由已知条件可得:CD=4x,根据勾股定理得:AD=5x,由AB=6且C在B点右侧,可以依次表示BC、CF、DF的长;
(2)分两种情况:
①当C在B点的右侧时,AF=DF,②当C在线段AB上时,又分两种情况:i)当CF<CD时,如图3,ii)当CF>CD时,如图4,由AF=DF,作等腰三角形的高线FN,由等腰三角形三线合一得:AN=ND=2.5x,利用同角的三角函数列比例式可求得x的值;
(3)先根据四边形DFD′G是平行四边形证明它为菱形,由角的关系得:AF平分∠DAC,作辅助线,由角平分线的性质得:FN=FC,根据第2问分两种情况进行计算,根据同角的三角函数列式可求得x的值.
解答 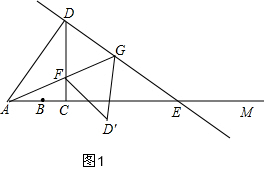 解:(1)∵CD=$\frac{4}{3}AC$,AC=3x,
解:(1)∵CD=$\frac{4}{3}AC$,AC=3x,
∴CD=4x,
∵CD⊥AM,
∴∠ACD=90°,
由勾股定理得:AD=5x,
∵AB=6,C在B点右侧,
∴BC=AC-AB=3x-6,
∵BC=FC=3x-6,
∴DF=CD-FC=4x-(3x-6)=x+6;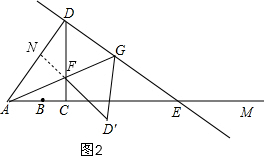
(2)分两种情况:
①当C在B点的右侧时,
∴AC>AB,
∴F必在线段CD上,
∵∠ACD=90°,
∴∠AFD是钝角,若△ADF为等腰三角形,只可能AF=DF,过F作FN⊥AD于N,如图2,
∴AN=ND=2.5x,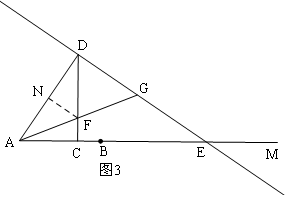
cos∠ADC=$\frac{DN}{DF}$=$\frac{DC}{AD}$,
$\frac{2.5x}{x+6}=\frac{4x}{5x}$,
x=$\frac{48}{17}$;
②当C在线段AB上时,同理可知若△ADF为等腰三角形,只可能AF=DF,
i)当CF<CD时,过F作FN⊥AD于N,如图3,
∵AB=6,AC=3x,
∴BC=CF=6-3x,
∴DF=4x-(6-3x)=7x-6,
cos∠ADC=$\frac{DN}{DF}=\frac{CD}{AD}$,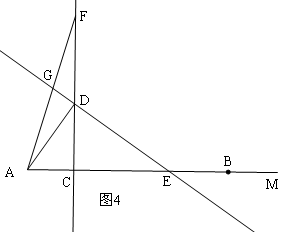
∴$\frac{2.5x}{7x-6}=\frac{4x}{5x}$,
x=$\frac{48}{31}$,
ii)当CF>CD时,如图4,
BC=CF=6-3x,
∴FD=AD=6-3x-4x=6-7x,
则6-7x=5x,
x=$\frac{1}{2}$,
综上所述,当x=$\frac{48}{17}$或$\frac{48}{31}$或$\frac{1}{2}$时,△AFD是等腰三角形;
(3)∵四边形DFD′G是平行四边形,且DF=D′F,
∴?DFD′G是菱形,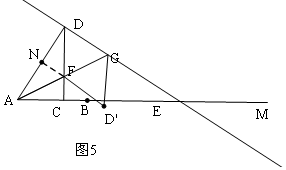
∴DF=DG,
∴∠DFG=∠DGF,
∵∠AFC=∠DFG,
∴∠DGF=∠AFC,
∵∠ACD=∠ADG=90°,
∴∠FAC=∠DAG,
即AF平分∠DAC,
过F作FN⊥AD于N,
当C在AB的延长线上时,如图2,FN=FC=3x-6,DF=x+6,
sin∠CDA=$\frac{3x-6}{x+6}=\frac{3}{5}$,
解得:x=4,
当C在AB边上时,如图5,FN=FC=6-3x,
DF=7x-6,
sin∠CDA=$\frac{6-3x}{7x-6}$=$\frac{3}{5}$,
x=$\frac{4}{3}$,
综上所述,若四边形DFD′G是平行四边形,x的值是4或$\frac{4}{3}$.
点评 本题是四边形的综合题,考查了平行四边形、菱形的性质和判定、等腰三角形的性质和判定、同角的三角函数以及动点问题,采用分类讨论的思想,并参考数形结合解决问题.


科目:初中数学 来源: 题型:解答题
 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
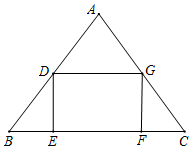 如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,S四边形DEFG=y.
如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,S四边形DEFG=y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2小时,已知摩托车行驶的路程s(千米)与行驶的时间t(时)之间的函数关系由下面的图象OBCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,则从甲地到乙地,这辆摩托车耗油量为0.9升,车修好后,摩托车的速度为30千米/小时.
如图所示,某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2小时,已知摩托车行驶的路程s(千米)与行驶的时间t(时)之间的函数关系由下面的图象OBCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,则从甲地到乙地,这辆摩托车耗油量为0.9升,车修好后,摩托车的速度为30千米/小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
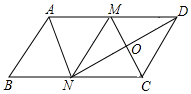 如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.
如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com