
分析 (1)先算乘法,再合并同类项,变形后代入求出即可;
(2)根据零指数幂、负整数指数幂、算术平方根、绝对值分别求出每一部分的值,再代入求出即可.
解答 解:(1)(x-2y)2-(x-y)(x+y)-2y2
=x2-4xy+4y2-x2+y2-2y2
=-4xy+3y2
=-y(4x-3y),
∵4x=3y,
∴4x-3y=0,
∴原式=-y×0=0;
(2)π0+2-1-$\sqrt{\frac{1}{4}}$-|-$\frac{1}{3}$|
=1+$\frac{1}{2}$-$\frac{1}{2}$-$\frac{1}{3}$
=$\frac{2}{3}$.
点评 本题考查了整式的混合运算和求值,也考查了实数的混合运算和零指数幂、负整数指数幂、算术平方根、绝对值等知识点,能熟记零指数幂、负整数指数幂、算术平方根、绝对值等知识点的内容是解(2)的关键,能正确根据整式的运算法则进行化简是解(1)的关键.


科目:初中数学 来源: 题型:解答题
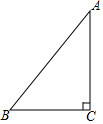 如图,已知Rt△ABC,∠C=90°,AC≠BC.
如图,已知Rt△ABC,∠C=90°,AC≠BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
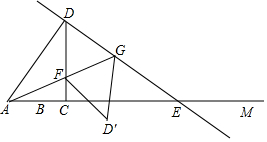 如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.
如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=$\frac{4}{3}$AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
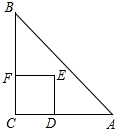 如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC上,C、D两点不重合,设CD的长度为x,Rt△ABC与正方形CDEF重叠部分的面积为y,则下列中能表示y与x之间的关系的是( )
如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC上,C、D两点不重合,设CD的长度为x,Rt△ABC与正方形CDEF重叠部分的面积为y,则下列中能表示y与x之间的关系的是( )| A. |  | B. | 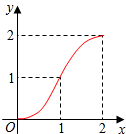 | C. | 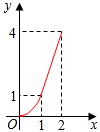 | D. | 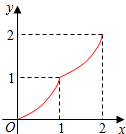 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 大小不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com