练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．先化简，再求值：$\frac{x}{1-x}+\frac{{x}^{2}-6x+9}{{x}^{2}-1}÷\frac{x-3}{x+1}$，其中x取-1、0、1、3中的一个值．

    分析 原式第二项利用除法法则变形，约分后两项通分并利用同分母分式的加法法则计算得到最简结果，把x的值代入计算即可求出值．

    解答 解：原式=-$\frac{x}{x-1}$+$\frac{（x-3）^{2}}{（x+1）（x-1）}$•$\frac{x+1}{x-3}$=-$\frac{x}{x-1}$+$\frac{x-3}{x-1}$=-$\frac{3}{x-1}$，
    当x=0时，原式=3．

    点评 此题考查了分式的化简求值，熟练掌握分式的加减乘除运算是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

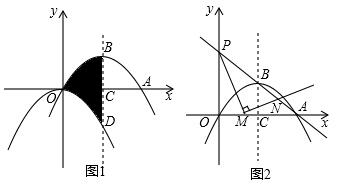
    13．如图所示，某人从甲地出发，骑摩托车去乙地，途中因车出现故障而停车修理，到达乙地时正好用了2小时，已知摩托车行驶的路程s（千米）与行驶的时间t（时）之间的函数关系由下面的图象OBCD给出，若这辆摩托车平均每行驶100千米的耗油量为2升，则从甲地到乙地，这辆摩托车耗油量为0.9升，车修好后，摩托车的速度为30千米/小时．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．（1）已知4x=3y，求代数式（x-2y）2-（x-y）（x+y）-2y2的值．
    （2）计算：π0+2-1-$\sqrt{\frac{1}{4}}$-|-$\frac{1}{3}$|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：（-1）2017+3（tan60°）-1-|1-$\sqrt{3}$|+（3.14-π）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知a、b互为相反数，c、d互为倒数，m的绝对值是5，n是最大的负整数，求代数式2016（a+b）-4cd+2mn的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图（1），抛物线 y=-$\frac{3}{16}$x2平移后过点A（8，0）和原点，顶点为B，对称轴与x轴相交于点C，与原抛物线相交于点D．

    （1）求平移后抛物线的解析式及点D的坐标；
    （2）直接写出阴影部分的面积 S阴影；
    （3）如图（2），直线AB与y轴相交于点P，点M为线段OA上一动点（点M不与点A，O重合 ），∠PMN为直角，MN与AP相交于点N，设OM=t，试探究：t为何值时，△MAN为等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．先化简：（1+$\frac{1}{x}$）÷$\frac{{x}^{2}-1}{x}$，再从1、-1、0、2中选择一个合适的数代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．一辆汽车开往距离出发地160km的目的地，出发后第一小时内按原计划的速度匀速行驶．一小时后以原来速度的1.5倍匀速行驶，比原计划提前20min到达目的地，求前一小时的行驶速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

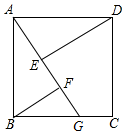    2．在边长为4cm的正方形ABCD中，点G是射线CB上的一点，E、F为直线AG上两个动点，连接DE、BF．
    （1）当DE⊥AG，BF⊥AG时，探索线段AF、BF、EF之间的数量关系式，并证明．
    （2）若点G在边BC上且BG=3cm，点E从A点以2cm/s的速度向G运动，同时点F从点G以1cm/s的速度向点A运动，（一个点到达终点，两个点同时停止），问当它们运动了多少秒后，S△DEF与S△BEF的差为$\frac{8}{5}$．

    查看答案和解析>>

    同步练习册答案