
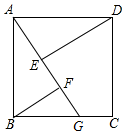
 在边长为4cm的正方形ABCD中,点G是射线CB上的一点,E、F为直线AG上两个动点,连接DE、BF.
在边长为4cm的正方形ABCD中,点G是射线CB上的一点,E、F为直线AG上两个动点,连接DE、BF.分析 (1)判定△ABF≌△DAE(AAS),即可得出AE=BF,再根据AF=AE+EF,即可得到AF=BF+EF;
(2)设△BEF中,EF边上的高为BP,△DEF中,EF边上的高为DQ,则BP=$\frac{12}{5}$,DQ=AP=$\frac{16}{5}$,再根据S△DEF与S△BEF的差为$\frac{8}{5}$,即可得出EF=4,设运动时间为t,根据线段的和差关系列出方程,求得t的值.
解答  解:(1)AF=BF+EF.
解:(1)AF=BF+EF.
理由:∵四边形ABCD为正方形,
∴AB=DA,∠DAB=90°,
又∵DE⊥AG,BF⊥AG,
∴∠AFB=∠DEA=90°,∠BAF=∠ADE,
在△ABF和△DAE中,
$\left\{\begin{array}{l}{∠AFB=∠DEA}\\{∠BAF=∠ADE}\\{AB=DA}\end{array}\right.$,
∴△ABF≌△DAE(AAS),
∴AE=BF,
又∵AF=AE+EF,
∴AF=BF+EF;
(2)∵BG=3cm,AB=4cm,
∴Rt△ABG中,AG=5cm,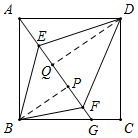
如图所示,设△BEF中,EF边上的高为BP,△DEF中,EF边上的高为DQ,则
BP=$\frac{AB×BG}{AG}$=$\frac{12}{5}$,DQ=AP=$\sqrt{A{B}^{2}-B{P}^{2}}$=$\frac{16}{5}$,
∵S△DEF与S△BEF的差为$\frac{8}{5}$,
∴$\frac{1}{2}$×EF×(DQ-BP)=$\frac{8}{5}$,
∴$\frac{1}{2}$×EF×($\frac{16}{5}$-$\frac{12}{5}$)=$\frac{8}{5}$,
∴EF=4,
设运动时间为t,
在E,F相遇之前,AG-AE-GF=EF,
∴5-t-2t=4,
解得t=$\frac{1}{3}$;
在E,F相遇之后,AE+GF-AG=EF,
∴t+2t-5=4,
解得t=3;
又∵5÷2=2.5s,
∴t≤2.5,
∴t=3不合题意,
故t的值为$\frac{1}{3}$s.
点评 本题主要考查了正方形的性质,勾股定理以及全等三角形的判定与性质的综合应用,解决问题的关键是根据全等三角形的对应边相等进行推导计算.解题时注意分类思想的运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
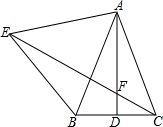 如图,△ABC中,AB=AC,AD是BC边上的中线,以AB为边向外作等边△ABE,与直线AD交于点F.
如图,△ABC中,AB=AC,AD是BC边上的中线,以AB为边向外作等边△ABE,与直线AD交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
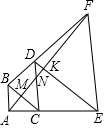 如图,以等腰直角△ABC的斜边BC为直角边向外作第二个等腰直角△BCD,再以等腰直角△BCD的斜边CD为直角边向外作第三个等腰直角△CDE,再以等腰直角△CDE的斜边DE为直角边向外作第四个等腰直角△DEF.连结AF分别交BC,DC,DE于点M,N,K,若S△ABM+S△DNK=13,则△CMN的面积为16.
如图,以等腰直角△ABC的斜边BC为直角边向外作第二个等腰直角△BCD,再以等腰直角△BCD的斜边CD为直角边向外作第三个等腰直角△CDE,再以等腰直角△CDE的斜边DE为直角边向外作第四个等腰直角△DEF.连结AF分别交BC,DC,DE于点M,N,K,若S△ABM+S△DNK=13,则△CMN的面积为16.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.
二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
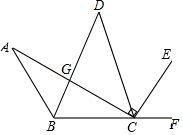 如图,AB∥CD,BD平分∠ABC,∠ACE=90°,AC⊥BD
如图,AB∥CD,BD平分∠ABC,∠ACE=90°,AC⊥BD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=45°.
校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com