
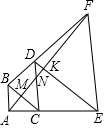
 如图,以等腰直角△ABC的斜边BC为直角边向外作第二个等腰直角△BCD,再以等腰直角△BCD的斜边CD为直角边向外作第三个等腰直角△CDE,再以等腰直角△CDE的斜边DE为直角边向外作第四个等腰直角△DEF.连结AF分别交BC,DC,DE于点M,N,K,若S△ABM+S△DNK=13,则△CMN的面积为16.
如图,以等腰直角△ABC的斜边BC为直角边向外作第二个等腰直角△BCD,再以等腰直角△BCD的斜边CD为直角边向外作第三个等腰直角△CDE,再以等腰直角△CDE的斜边DE为直角边向外作第四个等腰直角△DEF.连结AF分别交BC,DC,DE于点M,N,K,若S△ABM+S△DNK=13,则△CMN的面积为16. 分析 如图,由题意设AB=AC=a,则BC=BD=$\sqrt{2}$a,DC=CE=2a,DE=DF=2$\sqrt{2}$a,EF=4a,AF=$\sqrt{(3a)^{2}+(4a)^{2}}$=5a.由DN∥AB,推出$\frac{DN}{AB}$=$\frac{DF}{BF}$=$\frac{2\sqrt{2}a}{3\sqrt{2}a}$=$\frac{2}{3}$.推出DN=$\frac{2}{3}$a,CN=CD-DN=$\frac{4}{3}$a,由AB∥CD,CM∥DK,推出△ABM∽△NCM∽△NDK,推出$\frac{{S}_{△ABM}}{{S}_{△DNK}}$=$\frac{9}{4}$,$\frac{{S}_{△ABM}}{{S}_{△CMN}}$=$\frac{9}{16}$,由S△ABM+S△DNK=13,推出S△ABM=9,S△CMN=16.
解答 解:如图,由题意设AB=AC=a,则BC=BD=$\sqrt{2}$a,DC=CE=2a,DE=DF=2$\sqrt{2}$a,EF=4a,AF=$\sqrt{(3a)^{2}+(4a)^{2}}$=5a.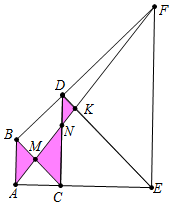
∵DN∥AB,
∴$\frac{DN}{AB}$=$\frac{DF}{BF}$=$\frac{2\sqrt{2}a}{3\sqrt{2}a}$=$\frac{2}{3}$.
∴DN=$\frac{2}{3}$a,CN=CD-DN=$\frac{4}{3}$a,
∵AB∥CD,CM∥DK,
∴△ABM∽△NCM∽△NDK,
∴$\frac{{S}_{△ABM}}{{S}_{△DNK}}$=$\frac{9}{4}$,$\frac{{S}_{△ABM}}{{S}_{△CMN}}$=$\frac{9}{16}$,
∵S△ABM+S△DNK=13,
∴S△ABM=9,S△CMN=16.
故答案为16.
点评 本题考查等腰直角三角形的性质、相似三角形的判定和性质等知识、解题的关键是学会利用参数解决问题,灵活运用相似三角形的性质,属于中考填空题中的压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
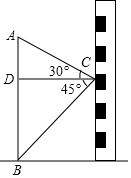 如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果精确到0.1米)
如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙O中,∠AOB=120°,点E在$\widehat{AB}$上任意一点,作等边△CDE,且C、D在AB上,设AC=x,BD=y,CD=2,则y关于x的函数关系式为y=$\frac{4}{x}$.
如图,⊙O中,∠AOB=120°,点E在$\widehat{AB}$上任意一点,作等边△CDE,且C、D在AB上,设AC=x,BD=y,CD=2,则y关于x的函数关系式为y=$\frac{4}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
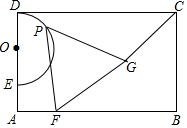 如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4$\sqrt{3}$,OD=2,点G在矩形内部,且∠GCB=30°,GC=2$\sqrt{3}$,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是4或6.
如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4$\sqrt{3}$,OD=2,点G在矩形内部,且∠GCB=30°,GC=2$\sqrt{3}$,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是4或6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
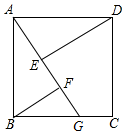 在边长为4cm的正方形ABCD中,点G是射线CB上的一点,E、F为直线AG上两个动点,连接DE、BF.
在边长为4cm的正方形ABCD中,点G是射线CB上的一点,E、F为直线AG上两个动点,连接DE、BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
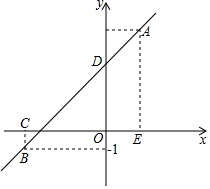 如图,一次函数的图象l经过点A(2,5),B(-4,-1)两点.
如图,一次函数的图象l经过点A(2,5),B(-4,-1)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com