
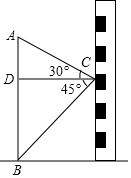
 如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果精确到0.1米)
如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果精确到0.1米)  每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5ab-ab=4 | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | a6÷a3=a3 | D. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
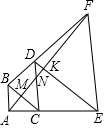 如图,以等腰直角△ABC的斜边BC为直角边向外作第二个等腰直角△BCD,再以等腰直角△BCD的斜边CD为直角边向外作第三个等腰直角△CDE,再以等腰直角△CDE的斜边DE为直角边向外作第四个等腰直角△DEF.连结AF分别交BC,DC,DE于点M,N,K,若S△ABM+S△DNK=13,则△CMN的面积为16.
如图,以等腰直角△ABC的斜边BC为直角边向外作第二个等腰直角△BCD,再以等腰直角△BCD的斜边CD为直角边向外作第三个等腰直角△CDE,再以等腰直角△CDE的斜边DE为直角边向外作第四个等腰直角△DEF.连结AF分别交BC,DC,DE于点M,N,K,若S△ABM+S△DNK=13,则△CMN的面积为16.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com