
| A. | 5ab-ab=4 | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | a6÷a3=a3 | D. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ |
分析 直接利用合并同类项法则以及二次根式加减运算法则和同底数幂的除法运算法则、分式加减运算法则分别化简求出答案.
解答 解:A、5ab-ab=4ab,故此选项错误,不合题意;
B、3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,故此选项错误,不合题意;
C、a6÷a3=a3,正确,符合题意;
D、$\frac{1}{a}$+$\frac{1}{b}$=$\frac{b}{ab}$+$\frac{a}{ab}$=$\frac{a+b}{ab}$,故此选项错误,不合题意;
故选:C.
点评 此题主要考查了合并同类项以及二次根式加减运算和同底数幂的除法运算、分式加减运算等知识,正确掌握运算法则是解题关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
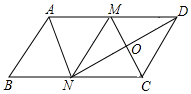 如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.
如图,在?ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
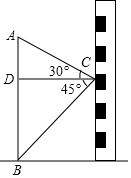 如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果精确到0.1米)
如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙O中,∠AOB=120°,点E在$\widehat{AB}$上任意一点,作等边△CDE,且C、D在AB上,设AC=x,BD=y,CD=2,则y关于x的函数关系式为y=$\frac{4}{x}$.
如图,⊙O中,∠AOB=120°,点E在$\widehat{AB}$上任意一点,作等边△CDE,且C、D在AB上,设AC=x,BD=y,CD=2,则y关于x的函数关系式为y=$\frac{4}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
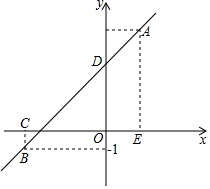 如图,一次函数的图象l经过点A(2,5),B(-4,-1)两点.
如图,一次函数的图象l经过点A(2,5),B(-4,-1)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com