
 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=45°.
校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=45°.分析 (1)分别在Rt△ADC与Rt△BDC中,利用正切函数,即可求得AD与BD的长,继而求得AB的长;
(2)由从A到B用时2秒,即可求得这辆校车的速度,比较与40千米/小时的大小,即可确定这辆校车是否超速.
解答 解:(1)由題意得,
在Rt△ADC中,AD=$\frac{CD}{tan30°}$=$\frac{30}{\frac{\sqrt{3}}{3}}$≈51.9(米),
在Rt△BDC中,BD=$\frac{CD}{tan45°}$=$\frac{30}{\frac{\sqrt{2}}{2}}$≈42.3(米),
则AB=AD-BD≈51.9-42.3=9.6(米);
(2)超速.
理由:∵汽车从A到B用时2秒,
∴速度为9.6÷2=4.8(米/秒),
∵4.8×3600=17280(米/时),
∴该车速度为17.28千米/小时,
∵小于40千米/小时,
∴这辆校车在AB路段不超速.
点评 此题考查了解直角三角形的应用问题.此题难度适中,解题的关键是把实际问题转化为数学问题求解,注意数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
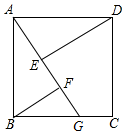 在边长为4cm的正方形ABCD中,点G是射线CB上的一点,E、F为直线AG上两个动点,连接DE、BF.
在边长为4cm的正方形ABCD中,点G是射线CB上的一点,E、F为直线AG上两个动点,连接DE、BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
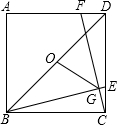 如图,正方形ABCD中,E,F分别为CD,AD上一点,CE=DF,BE,CF交于点G,O为BD的中点.
如图,正方形ABCD中,E,F分别为CD,AD上一点,CE=DF,BE,CF交于点G,O为BD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com