
分析 (1)根据多项式除以单项式可以解答本题;
(2)根据完全平方公式和平方差公式可以解答本题;
(3)根据积的乘方、单项式乘单项式和整式的加法可以解答本题;
(4)根据单项式乘多项式和整式的加减法可以解答本题.
解答 解:(1)(4x3-2x2-3x)÷(-3x)
=(4x3-2x2-3x)×($-\frac{1}{3x}$)
=$-\frac{4{x}^{2}}{3}+\frac{2x}{3}+1$;
(2)(2x-y)2-4(y-x)(-x-y)
=4x2-4xy+y2+4y2-4x2
=5y2-4xy;
(3)(2x3y)2•(-2xy)+(-2x3y)3÷(2x2)
=$(4{x}^{6}{y}^{2})•(-2xy)+(-8{x}^{9}{y}^{3})×\frac{1}{2{x}^{2}}$
=-8x7y3-4x7y3
=-12x7y3;
(4)2x(3x+5)-(2x+3)(3x-4)=2(3x+4)
去括号,得
6x2+10x-6x2-x+12=6x+8,
移项及合并同类项,得
3x=-4,
系数化为1,得
x=-$\frac{4}{3}$.
点评 本题考查整式的混合运算,解答本题的关键是明确整式的混合运算的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.
二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
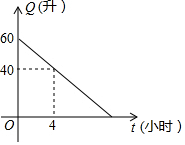 汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数,某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图所示,当油箱中余油20升时,该汽车行驶了8小时.
汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数,某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图所示,当油箱中余油20升时,该汽车行驶了8小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
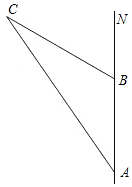 某轮船上午8时从A岛出发,以20海里/小时的速度向正北方向航行,如图,上午10时到达B岛,此时得到消息,在C岛周围15海里内有暗礁,经测量得∠NAC=15°,∠NBC=30°,问该轮船继续向北航行有无触礁危险?
某轮船上午8时从A岛出发,以20海里/小时的速度向正北方向航行,如图,上午10时到达B岛,此时得到消息,在C岛周围15海里内有暗礁,经测量得∠NAC=15°,∠NBC=30°,问该轮船继续向北航行有无触礁危险?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=45°.
校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=45°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2017次跳2017步就跳到了2号位置上.
如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2017次跳2017步就跳到了2号位置上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x>3\\ x>2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x>3\\ x<2\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<3\\ x>2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x<3\\ x<2\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
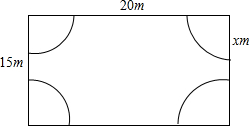 如图所示,某小区计划在一块长20米,宽15米的矩形荒地上建造一个花园,使得花园所占面积为荒地面积的一半,其中花园每个角上的扇形都相同,则每个扇形的半径x是多少?(精确到0.1)
如图所示,某小区计划在一块长20米,宽15米的矩形荒地上建造一个花园,使得花园所占面积为荒地面积的一半,其中花园每个角上的扇形都相同,则每个扇形的半径x是多少?(精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
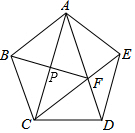 如图,正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,BF与AC交于点P.
如图,正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,BF与AC交于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com