练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．如图，有一颗棋子放在图中的1号位置上，现按顺时针方向，第一次跳一步到2号位置上第二次跳两步跳到4号位置上，第三次跳三步又跳到了1号位置上，第四次跳四步…一直进行下去，那么第2017次跳2017步就跳到了2号位置上．

    分析 棋子的跳法是有规律的，第一次跳1，第二次跳2，第三次跳3，…第N次跳N，则跳第N次后，棋子跳过的路程公式为：S=$\frac{（1+N）N}{2}$，棋子一个周期为6，设K=$\frac{S}{2}$，用K即可知道最后棋子的落位，若K为整数，则棋子落在1位；若K余1，则落2位，余2则落3位，余3则落4位，余4则落5位，余5则落6位．

    解答 解：∵第一次跳一步，第二次跳两步，第三次跳三步，第四次跳四步…第2014次跳2014步，
    ∴2014次总共跳：1+2+3+4+…+2017=$\frac{1}{2}$×2017×（2017+1）=2035153，
    2035153÷6=339192…1，
    ∵1步所对应的位置是2号位置，
    ∴第2017次跳2017步，所跳到的位置号是2号，
    故答案为：2．

    点评 此题考查图形的变化规律，找出数字之间的循环规律，利用规律解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．一次函数y=5x+3的图象是经过点（0，3）和（1，8）的一条直线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列运算中错误的是（　　）
    A．$\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$B．$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$C．2 $\sqrt{2}$+3$\sqrt{2}$=5$\sqrt{2}$D．$\sqrt{（\sqrt{2}-\sqrt{3}）^{2}}$=$\sqrt{2}-\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．正方形的边长为2，建立合适的直角坐标系，写出各个顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）计算：（4x3-2x2-3x）÷（-3x）；
    （2）计算：（2x-y）2-4（y-x）（-x-y）；
    （3）计算：（2x3y）2•（-2xy）+（-2x3y）3÷（2x2）；
    （4）解方程：2x（3x+5）-（2x+3）（3x-4）=2（3x+4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，已知点O是直线AB上一点，∠1=65°，则∠2的度数（　　）
    A．25°B．65°C．105°D．115°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．观察下表，按你发现的规律填空
    a0.01211.2112112100
    $\sqrt{a}$0.111.111110
    已知$\sqrt{15}$=3.873，则$\sqrt{150000}$的值为387.3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

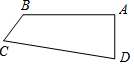    11．如图，四边形ABCD中，AB⊥AD于A，AB=8$\sqrt{6}$，AD=8$\sqrt{3}$，BC=7，CD=25，则四边形ABCD的面积为84+96$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

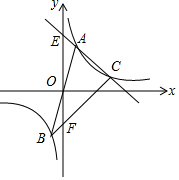    12．如图，已知直线y=3x与反比例函数y=$\frac{k}{x}$的图象交于A，B两点，其中A（1，3），点C是反比例函数在第一象限的图象上不同于A的一点，直线AC交y轴于点E，直线BC交y轴于点F，则线段EF的长是（　　）
    A．4B．5C．6D．变量

    查看答案和解析>>

    同步练习册答案