
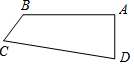
 如图,四边形ABCD中,AB⊥AD于A,AB=8$\sqrt{6}$,AD=8$\sqrt{3}$,BC=7,CD=25,则四边形ABCD的面积为84+96$\sqrt{2}$.
如图,四边形ABCD中,AB⊥AD于A,AB=8$\sqrt{6}$,AD=8$\sqrt{3}$,BC=7,CD=25,则四边形ABCD的面积为84+96$\sqrt{2}$. 分析 连接BD,在Rt△ABD中,已知AB,AD的长,运用勾股定理可求出BD的长,在△BCD中,已知三边长,运用勾股定理逆定理,可得此三角形为直角三角形,故四边形ABCD的面积为Rt△ABD与Rt△CBD的面积之和.
解答 解:连接BD,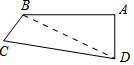
∵AB⊥AD,
∴∠A=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=24,
∵BC2+BD2=72+242=625=252=CD2,
∴△CBD为直角三角形,
∴S四边形ABCD=S△ABD+S△BCD
=$\frac{1}{2}$×8$\sqrt{6}$×8$\sqrt{3}$+$\frac{1}{2}$×24×7
=96$\sqrt{2}$+84.
点评 本题考查的是勾股定理的逆定理及三角形的面积公式,根据题意作出辅助线,判断出△CBD的形状是解答此题的关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:填空题
 如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2017次跳2017步就跳到了2号位置上.
如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2017次跳2017步就跳到了2号位置上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
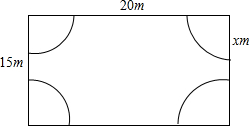 如图所示,某小区计划在一块长20米,宽15米的矩形荒地上建造一个花园,使得花园所占面积为荒地面积的一半,其中花园每个角上的扇形都相同,则每个扇形的半径x是多少?(精确到0.1)
如图所示,某小区计划在一块长20米,宽15米的矩形荒地上建造一个花园,使得花园所占面积为荒地面积的一半,其中花园每个角上的扇形都相同,则每个扇形的半径x是多少?(精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com