
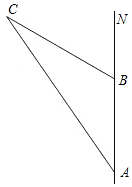
 某轮船上午8时从A岛出发,以20海里/小时的速度向正北方向航行,如图,上午10时到达B岛,此时得到消息,在C岛周围15海里内有暗礁,经测量得∠NAC=15°,∠NBC=30°,问该轮船继续向北航行有无触礁危险?
某轮船上午8时从A岛出发,以20海里/小时的速度向正北方向航行,如图,上午10时到达B岛,此时得到消息,在C岛周围15海里内有暗礁,经测量得∠NAC=15°,∠NBC=30°,问该轮船继续向北航行有无触礁危险?  七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
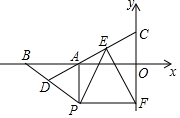 已知:如图,平面直角坐标系中,点B坐标为(-4,0),点A为线段OB中点,点P在第三象限,且AP⊥y轴,PF⊥y轴,D为BP中点,连接DA并延长交y轴于点C,FE⊥DC.
已知:如图,平面直角坐标系中,点B坐标为(-4,0),点A为线段OB中点,点P在第三象限,且AP⊥y轴,PF⊥y轴,D为BP中点,连接DA并延长交y轴于点C,FE⊥DC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | C. | 2 $\sqrt{2}$+3$\sqrt{2}$=5$\sqrt{2}$ | D. | $\sqrt{(\sqrt{2}-\sqrt{3})^{2}}$=$\sqrt{2}-\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| a | 0.0121 | 1.21 | 121 | 12100 |
| $\sqrt{a}$ | 0.11 | 1.1 | 11 | 110 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com