
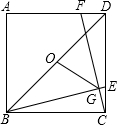
 如图,正方形ABCD中,E,F分别为CD,AD上一点,CE=DF,BE,CF交于点G,O为BD的中点.
如图,正方形ABCD中,E,F分别为CD,AD上一点,CE=DF,BE,CF交于点G,O为BD的中点.分析 (1)根据四边形ABCD是正方形,判定△BCE≌△CDF(SAS),可得∠CBE=∠DCF,再根据∠BCG+∠DCF=90°,得出∠BCG+∠CBE=90°,进而得到∠BGC=90°,即BE⊥CF;
(2)连接OC,过O作OH⊥OG,交BE于H,根据∠BOC=∠BGC=90°,可得B、O、G、C四点共圆,进而得到∠OGB=∠OCB=45°,即△OGH是等腰直角三角形,进而得出HG=$\sqrt{2}$OG,再判定△BOH≌△COG(SAS),得出BH=CG,最后根据BG-BH=HG,即可得到BG-CG=$\sqrt{2}$OG.
解答 解:(1)∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠CDF=90°,
在△BCE和△CDF中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCD=∠CDF}\\{CE=DF}\end{array}\right.$,
∴△BCE≌△CDF(SAS),
∴∠CBE=∠DCF,
又∵∠BCG+∠DCF=90°,
∴∠BCG+∠CBE=90°,
∴∠BGC=90°,即BE⊥CF;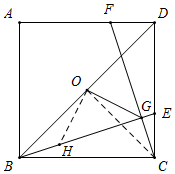
(2)如图,连接OC,过O作OH⊥OG,交BE于H,
∵O为BD的中点,即O为正方形的对称中心,
∴△BOC是等腰直角三角形,
∴∠BOC=∠BGC=90°,
∴B、O、G、C四点共圆,
∴∠OGB=∠OCB=45°,
∴△OGH是等腰直角三角形,
∴HG=$\sqrt{2}$OG,HO=GO,
∵∠BOC=∠GOH=90°,
∴∠BOH=∠COG,
在△BOH和△COG中,
$\left\{\begin{array}{l}{BO=CO}\\{∠BOH=∠COG}\\{HO=GO}\end{array}\right.$,
∴△BOH≌△COG(SAS),
∴BH=CG,
又∵BG-BH=HG,
∴BG-CG=$\sqrt{2}$OG.
点评 本题主要考查了正方形的性质,全等三角形的判定与性质以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线构造等腰直角三角形以及全等三角形,依据全等三角形的对应边相等进行求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
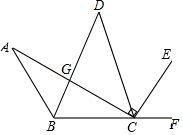 如图,AB∥CD,BD平分∠ABC,∠ACE=90°,AC⊥BD
如图,AB∥CD,BD平分∠ABC,∠ACE=90°,AC⊥BD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=45°.
校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如图检测公路上行驶的校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=45°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x>3\\ x>2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x>3\\ x<2\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<3\\ x>2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x<3\\ x<2\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.15×107 | B. | 0.15×108 | C. | 1.5×107 | D. | 1.5×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
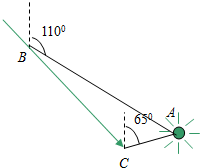 如图,货轮在海上自B点沿方位角(指从北按顺时针转到目标线的角度)140°的方向航行,为了确定船位,船在B点观测灯塔A的方位角为110°,船到达C点,观测灯塔A的方位是65°,求AB与AC的夹角是多少?
如图,货轮在海上自B点沿方位角(指从北按顺时针转到目标线的角度)140°的方向航行,为了确定船位,船在B点观测灯塔A的方位角为110°,船到达C点,观测灯塔A的方位是65°,求AB与AC的夹角是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com