
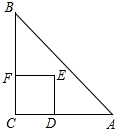
 如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC上,C、D两点不重合,设CD的长度为x,Rt△ABC与正方形CDEF重叠部分的面积为y,则下列中能表示y与x之间的关系的是( )
如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC上,C、D两点不重合,设CD的长度为x,Rt△ABC与正方形CDEF重叠部分的面积为y,则下列中能表示y与x之间的关系的是( )| A. |  | B. | 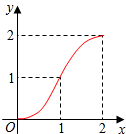 | C. |  | D. |  |
分析 分类讨论:当0<x≤1时,根据正方形的面积公式得到y=x2;当1<x≤2时,ED交AB于M,EF交AB于N,利用重叠的面积等于正方形的面积减去等腰直角三角形MNE的面积得到y=x2-2(x-1)2,配方得到y=-(x-2)2+2,然后根据二次函数的性质对各选项进行判断.
解答 解:当0<x≤1时,y=x2,
当1<x≤2时,ED交AB于M,EF交AB于N,如图,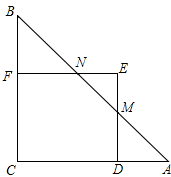 CD=x,则AD=2-x,
CD=x,则AD=2-x,
∵Rt△ABC中,AC=BC=2,
∴△ADM为等腰直角三角形,
∴DM=2-x,
∴EM=x-(2-x)=2x-2,
∴S△ENM=$\frac{1}{2}$(2x-2)2=2(x-1)2,
∴y=x2-2(x-1)2=-x2+4x-2=-(x-2)2+2,
∴y=$\left\{\begin{array}{l}{{x}^{2},(0<x≤1)}\\{-(x-2)^{2}+2,(1<x≤2)}\end{array}\right.$.
故选:B.
点评 本题考查了动点问题的函数图象:通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.也考查了等腰直角三角形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
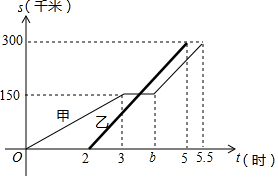 甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com