
【题目】如图,∠ABC=60°,∠1=∠2.
(1)求∠3的度数;
(2)若AD⊥BC,AF=6,求DF的长.
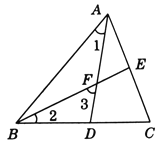
【答案】(1)60°;(2)3
【解析】
(1)由三角形的外角性质,得到∠3=∠1+∠ABF,由∠1=∠2,得到∠3=∠ABC,即可得到答案;
(2)由(1)∠3=∠ABC=60°,由AD⊥BC,则∠2=∠1=30°,则∠ABF=30°=∠1,则BF=AF=6,即可求出DF的长度.
解:(1)根据题意,由三角形的外角性质,得
∠3=∠1+∠ABF,
∵∠1=∠2,
∴∠3=∠2+∠ABF,
∵∠ABC=∠ABF+∠2=60°,
∴∠3=60°;
(2)由(1)可知,∠3=60°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠2=30°,
∴![]() ,
,
∵∠3=∠2+∠ABF,
∴∠ABF=30°,
∵∠1=∠2=30°,
∴∠ABF=∠1=30°,
∴BF=AF=6,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】![]() 分别是三角形
分别是三角形![]() 的边
的边![]() 的中点,
的中点,![]() 是
是![]() 所在平面上的动点,连接
所在平面上的动点,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点,顺次连接点
的中点,顺次连接点![]()

(1)如图,当点![]() 在
在![]() 的内部时,求证:四边形
的内部时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若四边形![]() 是菱形,则
是菱形,则![]() 与
与![]() 应满足怎样的关系?若四边形
应满足怎样的关系?若四边形![]() 是矩形,则
是矩形,则![]() 与
与![]() 应满足怎样的关系?(直接写出答案,不需要说明理由)
应满足怎样的关系?(直接写出答案,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(ab)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若m+n=5,mn=4,则mn= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点D,下列结论:①△BCD是等腰三角形;②BD是∠ABC的平分线;③DC+BC=AB;④△AMD≌△BCD,正确的是 ( )

A.①②B.②③C.①②③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
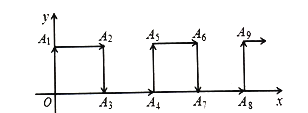
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点
出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点![]() ,
,![]() ,
,![]() ,
,![]() ,...那么点
,...那么点![]() 的坐标为( ).
的坐标为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() 于点
于点![]() 于点
于点![]() ,
,![]() 为
为![]() 边的中点,连接
边的中点,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() 为等边三角形;④当
为等边三角形;④当![]() 时,
时,![]() .其中正确的是____________(填写序号).
.其中正确的是____________(填写序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com