
如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.
(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);
(2)设△MNC与△OAB重叠部分的面积为S.
①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.

(1)( ,
, ),P(0,2t),Q(t,0);(2)①
),P(0,2t),Q(t,0);(2)① ;②当t=1时,S有最大值,最大值为1.
;②当t=1时,S有最大值,最大值为1.
【解析】
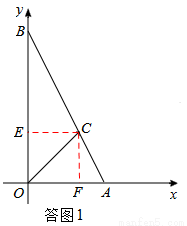
试题分析:(1)如答图1,作辅助线,由比例式求出点D的坐标;
(2)①所求函数关系式为分段函数,需要分类讨论:答图2,答图3表示出运动过程中重叠部分(阴影)的变化,分别求解.
②画出函数图象,由两段抛物线构成.观察图象,可知当t=1时,S有最大值.
试题解析:【解析】
(1)如答图1,过点C作CF⊥x轴于点F,CE⊥y轴于点E,
由题意,易知四边形OECF为正方形,设正方形边长为x.
∵CE∥x轴,∴△BEC∽△BOA.∴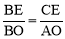 ,即
,即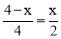 ,解得x=
,解得x=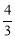 .
.
∴C点坐标为(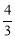 ,
,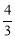 ).
).
∵PQ∥AB,∴ ,即
,即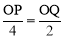 .
.
∴OP=2OQ.
∵P(0,2t),∴Q(t,0).
∵对称轴OC为第一象限的角平分线,∴对称点坐标为:M(2t,0),N(0,t).
(2)①当0<t≤1时,如答图2所示,点M在线段OA上,重叠部分面积为S△CMN.
S△CMN=S四边形CMON﹣S△OMN=(S△COM+S△CON)﹣S△OMN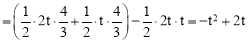 .
.
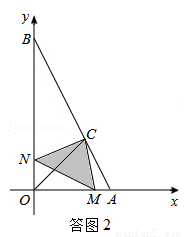
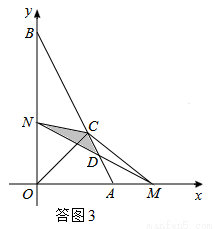
当1<t<2时,如答图3所示,点M在OA的延长线上,
设MN与AB交于点D,则重叠部分面积为S△CDN.
设直线MN的解析式为y=kx+b,
将M(2t,0)、N(0,t)代入得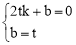 ,解得
,解得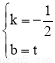 .
.
∴直线MN的解析式为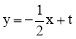 .
.
同理求得直线AB的解析式为:y=﹣2x+4.
联立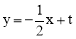 与y=﹣2x+4,求得点D的横坐标为
与y=﹣2x+4,求得点D的横坐标为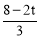 .
.
S△CDN=S△BDN﹣S△BCN=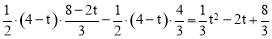 .
.
综上所述,S关于t的函数关系式为 .
.
②画出函数图象,如答图4所示:
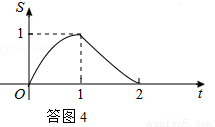
观察图象,可知当t=1时,S有最大值,最大值为1.
考点:1.双动点和轴对称问题;2.正方形的判定和性质;3.相似三角形的判定和性质;4.直线上点的坐标与方程的关系;5.待定系数法的应用;6.由实际问题列函数关系式;7.分类思想、数形结合思想和方程思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014年初中毕业升学考试(江苏淮安卷)数学(解析版) 题型:填空题
一只不透明的袋子中装有1个白球和3个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,则摸出红球的概率为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏淮安卷)数学(解析版) 题型:选择题
如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )

A.5[来源: B.6 C.7 D.25
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:解答题
为了解“数学思想作文对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表来表示(图、表都没制作完成).
选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
人数 | a | 543 | 269 | b |
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值.
(注:计算中涉及到的“人数”均精确到1)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:填空题
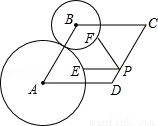
如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最小值是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:填空题
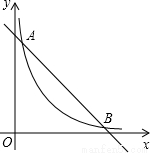
在平面直角坐标系xOy中,一次函数 的图象与函数
的图象与函数 的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .
的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com