
 如图,用十字形方框从日历表中框出5个数,已知这5个数的和为5a-5,a是方框①,②,③,④中的一个数,则数a所在的方框是( )
如图,用十字形方框从日历表中框出5个数,已知这5个数的和为5a-5,a是方框①,②,③,④中的一个数,则数a所在的方框是( )| A. | ① | B. | ② | C. | ③ | D. | ④ |
分析 解法一:设中间位置的数为A,由此可表示上下左右四个位置的数,相加可得a的值;
解法二:可以把5a-5因式分解成5(a-1),中间的数就是a-1,所以3号就是a
解答 解:解法一:设中间位置的数为A,则①位置数为:A-7,④位置为:A+7,左②位置为:A-1,右③位置为:A+1,其和为5A=5a-5,
∴a=A+1,
即a为③位置的数;
解法二:5a-5=5(a-1),
则中间的数为a-1,
因为方框③表示的数比中间的数大1,
所以方程③表示的数就是a,即数a所在的方框就是③;
故选C.
点评 本题是日历上的数,明确日历上的规律是关键:上下两数的差为7,左右两数的差为1;解答时要细心表示方框中的数,容易书写错误.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}}$=($\sqrt{x}$)2 | B. | $\root{3}{{x}^{3}}$=$\sqrt{{x}^{2}}$ | C. | $\sqrt{{(-x)}^{2}}$=|-x| | D. | $\sqrt{{x}^{2}-4}$=$\sqrt{x+2}$•$\sqrt{x-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
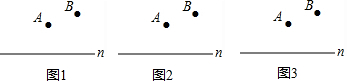
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
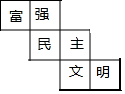 如图,是每个面上都标有一个汉字的正方体的平面展开图,在此正方体上与“民”字相对的面上的汉字是( )
如图,是每个面上都标有一个汉字的正方体的平面展开图,在此正方体上与“民”字相对的面上的汉字是( )| A. | “富” | B. | “强” | C. | “文” | D. | “明” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com