
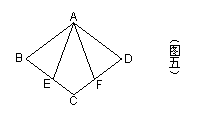
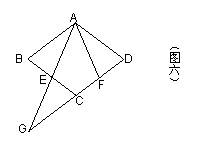
已知:如图五,在平行四边形ABCD中,点E、F
分别在BC、CD上,且AE=AF,∠AEC=∠AFC.
(1)求证:四边形ABCD是菱形;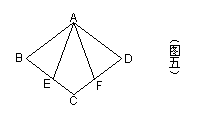
(2)如图六,若AD=AF,延长AE、DC交于点
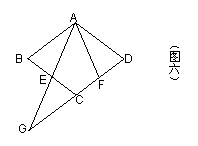 G,求证:AF2=AG·DF.
G,求证:AF2=AG·DF.
(3)在第(2 )小题的条件下,连接BD,交AG
)小题的条件下,连接BD,交AG
于点H,若HE=4,EG=12,求AH的长.
(1)证明:∵四边形ABCD是平行四边形,
 ∴∠B=∠D.…………………(1分)
∴∠B=∠D.…………………(1分)
∵∠AEC=∠AFC,∠AEC+∠AEB=∠AFC+∠AFD=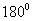
∴∠AEB=∠AFD.…………(1分)
在△AEB和△AFD中:
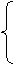 ∠B=∠D
∠B=∠D
∠AEB=∠AFD
AE=AF
∴△AEB≌△AFD,………………(1分)
∴AB=AD,
∴平行四边形ABCD是菱形.………………(1分)
(2)∵△AEB≌△AFD,∴∠BAE=∠DAF.
∵四边形ABCD是平行四边形,∴AB∥DG, ∴∠BAE=∠G,
 ∴∠G=∠DAF.
∴∠G=∠DAF.
又∵∠ADF=∠GDA,∴△GAD∽△AFD………………(2分)
∴DA︰DF=DG︰DA,∴DA2=DG·DF……………(1分)
∵DG︰DA=AG︰FA,且AD=AF,∴DG=AG.
又∵AD=AF,∴AF2=AG·DF.……………………(1分)
(3)在菱形ABCD中,∵AB∥DC,AD∥BC,
∴AH︰HG =BH︰HD,………………(1分)
=BH︰HD,………………(1分)
BH︰HD=EH︰AH,………………(1分)
∴AH︰HG=EH︰AH.………………(1分)
∵HE=4,EG=12,
∴AH︰16=4︰AH,∴AH=8.………………(1分)


科目:初中数学 来源: 题型:
下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为( )

A.21 B.24 C.27 D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
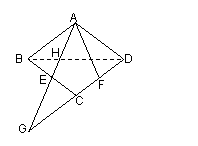
如图三,在Rt△ABC中,∠ACB=90°,将△ABC
沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,
再将其沿DE折叠,使点A落在DC′的延长线上的A′
处,若△BED与△ABC相似 ,则相似比
,则相似比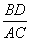 = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com