
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊе§ЗНаЮABCDЕФБпГЄЮЊ1ЃЌЕуEдкБпBCЩЯЃЌШєЁЯAEF=900ЃЌЧвEFНЛе§ЗНаЮЭтНЧЕФЦНЗжЯпCFгкЕуF
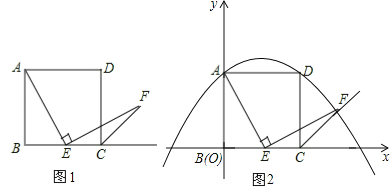
ЃЈ1ЃЉЭМ1жаШєЕуEЪЧБпBCЕФжаЕуЃЌЮвУЧПЩвдЙЙдьСНИіШ§НЧаЮШЋЕШРДжЄУїAE=EFЃЌЧыа№ЪіФуЕФвЛИіЙЙдьЗНАИЃЌВЂжИГіЪЧФФСНИіШ§НЧаЮШЋЕШЃЈВЛвЊЧѓжЄУїЃЉЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєЕуEдкЯпЖЮBCЩЯЛЌЖЏЃЈВЛгыЕуBЃЌCжиКЯЃЉЃЎ
ЂйAE=EFЪЧЗёзмГЩСЂЃПЧыИјГіжЄУїЃЛ
ЂкдкШчЭМ2ЕФжБНЧзјБъЯЕжаЃЌЕБЕуEЛЌЖЏЕНФГДІЪБЃЌЕуFЧЁКУТфдкХзЮяЯп![]() ЩЯЃЌЧѓДЫЪБЕуFЕФзјБъЃЎ
ЩЯЃЌЧѓДЫЪБЕуFЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЁїAGEгыЁїECFЃЈ2ЃЉЂйГЩСЂЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉШЁABЕФжаЕуGЃЌСЌНгEGЃЌРћгУASAФмЕУЕНЁїAGEгыЁїECFШЋЕШЃЎ
ЃЈ2ЃЉЂйдкABЩЯНиШЁAG=ECЃЌгЩASAжЄЕУЁїAGEЁеЁїECFМДПЩжЄЕУAE=EFЃЎ
ЂкЙ§ЕуFзїFHЁЭxжсгкHЃЌИљОнFH=BE=CHЩшBH=aЃЌдђFH=aЃ1ЃЌШЛКѓБэЪОГіЕуFЕФзјБъЃЌИљОнЕуFЧЁКУТфдкХзЮяЯп![]() ЩЯЕУЕНгаЙиaЕФЗНГЬЧѓЕУaжЕМДПЩЧѓЕУЕуFЕФзјБъЃЎ
ЩЯЕУЕНгаЙиaЕФЗНГЬЧѓЕУaжЕМДПЩЧѓЕУЕуFЕФзјБъЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌШЁABЕФжаЕуGЃЌСЌНгEGЃЌдђЁїAGEгыЁїECFШЋЕШЃЎ

ЃЈ2ЃЉЂйШєЕуEдкЯпЖЮBCЩЯЛЌЖЏЪБAE=EFзмГЩСЂЃЎжЄУїШчЯТЃКШчЭМЃЌ
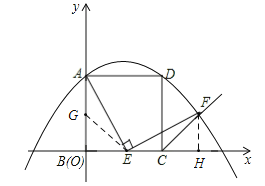
дкABЩЯНиШЁAG=ECЃЌ
ЁпAB=BCЃЌ
ЁрBG=BEЃЎ
ЁрЁїGBEЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЁрЁЯAGE=180ЁуЃ45Ёу=135ЁуЃЎ
гжЁпCFЦНЗже§ЗНаЮЕФЭтНЧЃЌ
ЁрЁЯECF=135ЁуЃЎ
ЁрЁЯAGE=ЁЯECFЃЎ
гжЁпЁЯBAE+ЁЯAEB=ЁЯCEF+ЁЯAEB=90ЁуЃЌ
ЁрЁЯBAE=ЁЯCEFЃЎ
ЁрЁїAGEЁеЁїECFЃЈASAЃЉЃЎ
ЁрAE=EFЃЎ
ЂкЙ§ЕуFзїFHЁЭxжсгкHЃЌ
гЩЂйжЊЃЌFH=BE=CHЃЌЩшBH=aЃЌдђFH=aЃ1ЃЎ
ЁрЕуFЕФзјБъЮЊFЃЈaЃЌaЃ1ЃЉЃЎ
ЁпЕуFЧЁКУТфдкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёрa2=2ЃЎЁр![]() ЃЈИКжЕВЛКЯЬтвтЃЌЩсШЅЃЉЃЎ
ЃЈИКжЕВЛКЯЬтвтЃЌЩсШЅЃЉЃЎ
Ёр![]() ЃЎЁрЕуFЕФзјБъЮЊ
ЃЎЁрЕуFЕФзјБъЮЊ![]() ЃЎ
ЃЎ


 ЮФОДЭМЪщПЮЪБЯШЗцЯЕСаД№АИ
ЮФОДЭМЪщПЮЪБЯШЗцЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌбЇаЃзМБИдкНЬбЇТЅКѓУцДюНЈвЛИіМђвзОиаЮздааГЕГЕХяЃЌвЛБпРћгУНЬбЇТЅЕФКѓЧН(ПЩРћгУЕФЧНГЄЮЊ19 m)ЃЌСэЭтШ§БпРћгУбЇаЃЯжгазмГЄ38 mЕФЬњРИЮЇГЩЃЎ
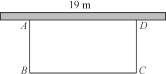
(1)ШєЮЇГЩЕФУцЛ§ЮЊ180 m2ЃЌЪдЧѓГіздааГЕГЕХяЕФГЄКЭПэЃЛ
(2)ФмЮЇГЩУцЛ§ЮЊ200 m2ЕФздааГЕГЕХяТ№ЃПШчЙћФмЃЌЧыФуИјГіЩшМЦЗН,ШчЙћВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊAЃЌBЪЧЗДБШР§КЏЪ§y=![]() ЃЈkЃО0ЃЌxЃО0ЃЉЭМЯѓЩЯЕФСНЕуЃЌBCЁЮxжсЃЌНЛyжсгкЕуCЃЌЖЏЕуPДгзјБъдЕуOГіЗЂЃЌбиOЁњAЁњBЁњCЃЈЭМжаЁАЁњЁБЫљЪОТЗЯпЃЉдШЫйдЫЖЏЃЌжеЕуЮЊCЃЌЙ§PзїPMЁЭxжсЃЌДЙзуЮЊMЃЎЩшШ§НЧаЮOMPЕФУцЛ§ЮЊSЃЌPЕудЫЖЏЪБМфЮЊtЃЌдђSЙигкxЕФКЏЪ§ЭМЯѓДѓжТЮЊЃЈ ЃЉ
ЃЈkЃО0ЃЌxЃО0ЃЉЭМЯѓЩЯЕФСНЕуЃЌBCЁЮxжсЃЌНЛyжсгкЕуCЃЌЖЏЕуPДгзјБъдЕуOГіЗЂЃЌбиOЁњAЁњBЁњCЃЈЭМжаЁАЁњЁБЫљЪОТЗЯпЃЉдШЫйдЫЖЏЃЌжеЕуЮЊCЃЌЙ§PзїPMЁЭxжсЃЌДЙзуЮЊMЃЎЩшШ§НЧаЮOMPЕФУцЛ§ЮЊSЃЌPЕудЫЖЏЪБМфЮЊtЃЌдђSЙигкxЕФКЏЪ§ЭМЯѓДѓжТЮЊЃЈ ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
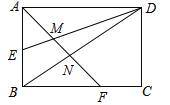
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDЕФБпГЄAD=3ЃЌAB=2ЃЌEЮЊABЕФжаЕуЃЌFдкБпBCЩЯЃЌЧвBF=2FCЃЌAFЗжБ№гыDEЁЂDBЯрНЛгкЕуMЃЌNЃЌдђMNЕФГЄЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓЕФЖЅЕудкЕквЛЯѓЯоЃЌЧвЙ§ЕуЃЈ0ЃЌ1ЃЉКЭЃЈЉ1ЃЌ0ЃЉЃЎЯТСаНсТлЃКЂйabЃМ0ЃЌЂкb2ЃО4aЃЌЂл0ЃМa+b+cЃМ2ЃЌЂм0ЃМbЃМ1ЃЌЂнЕБxЃОЉ1ЪБЃЌyЃО0ЃЌЦфжае§ШЗНсТлЕФИіЪ§ЪЧ
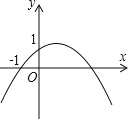
AЃЎ5Иі BЃЎ4Иі CЃЎ3Иі DЃЎ2Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
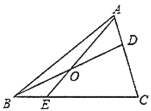
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() дк
дк![]() БпЩЯЃЌ
БпЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() гк
гк![]() ЃЌдђ
ЃЌдђ![]() ______ЃЎ
______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШчЙћШ§НЧаЮЕФСНИіФкНЧ![]() гы
гы![]() Тњзу
Тњзу![]() ЃЌФЧУДГЦетбљЕФШ§НЧаЮЮЊЁАРржБНЧШ§НЧаЮЁБЃЎ
ЃЌФЧУДГЦетбљЕФШ§НЧаЮЮЊЁАРржБНЧШ§НЧаЮЁБЃЎ
ГЂЪддЫгУ
ЃЈ1ЃЉШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФЦНЗжЯпЃЎ
ЕФЦНЗжЯпЃЎ
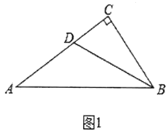
ЂйжЄУї![]() ЪЧЁАРржБНЧШ§НЧаЮЁБЃЛ
ЪЧЁАРржБНЧШ§НЧаЮЁБЃЛ
ЂкЪдЮЪдкБп![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЈвьгкЕу
ЃЈвьгкЕу![]() ЃЉЃЌЪЙЕУ
ЃЉЃЌЪЙЕУ![]() вВЪЧЁАРржБНЧШ§НЧаЮЁБЃПШєДцдкЃЌЧыЧѓГі
вВЪЧЁАРржБНЧШ§НЧаЮЁБЃПШєДцдкЃЌЧыЧѓГі![]() ЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
РрБШЭиеЙ
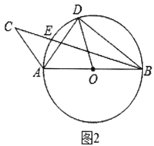
ЃЈ2ЃЉШчЭМ2ЃЌ![]() ФкНггк
ФкНггк![]() ЃЌжБОЖ
ЃЌжБОЖ![]() ЃЌЯв
ЃЌЯв![]() ЃЌЕу
ЃЌЕу![]() ЪЧЛЁ
ЪЧЛЁ![]() ЩЯвЛЖЏЕуЃЈАќРЈЖЫЕу
ЩЯвЛЖЏЕуЃЈАќРЈЖЫЕу![]() ЃЌ
ЃЌ![]() ЃЉЃЌбгГЄ
ЃЉЃЌбгГЄ![]() жСЕу
жСЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌЧв
ЃЌЧв![]() ЃЌЕБ
ЃЌЕБ![]() ЪЧЁАРржБНЧШ§НЧаЮЁБЪБЃЌЧѓ
ЪЧЁАРржБНЧШ§НЧаЮЁБЪБЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуPЪЧСтаЮABCDЕФЖдНЧЯпBDЩЯвЛЕуЃЌСЌНгCPВЂбгГЄЃЌНЛADгкEЃЌНЛBAЕФбгГЄЯпгкЕуF.
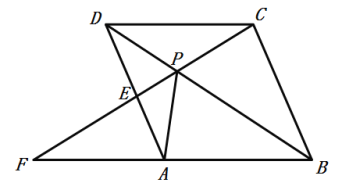
ЃЈ1ЃЉЧѓжЄЃК![]() .
.
ЃЈ2ЃЉШчЙћ![]() ЃЌЧѓЯпЖЮPCЕФГЄ.
ЃЌЧѓЯпЖЮPCЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
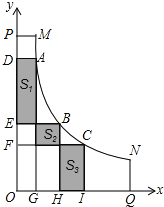
ЁОЬтФПЁПСљвЛЖљЭЏНкЃЌаЁЮФЕНЙЋдАгЮЭцЃЎПДЕНЙЋдАЕФвЛЖЮШЫааЭфЕРMNЃЈВЛМЦПэЖШЃЉЃЌШчЭМЃЌЫќгыСНУцЛЅЯрДЙжБЕФЮЇЧНOPЁЂOQжЎМфгавЛПщПеЕиMPOQNЃЈMPЁЭOPЃЌNQЁЭOQЃЉЃЌЫћЗЂЯжЭфЕРMNЩЯШЮвЛЕуЕНСНБпЮЇЧНЕФДЙЯпЖЮгыЮЇЧНЫљЮЇГЩЕФОиаЮЕФУцЛ§ЖМЯрЕШЃЌБШШчЃКAЁЂBЁЂCЪЧЭфЕРMNЩЯЕФШ§ЕуЃЌОиаЮADOGЁЂОиаЮBEOHЁЂОиаЮCFOIЕФУцЛ§ЯрЕШЃЎАЎКУЪ§бЇЕФЫћНЈСЂСЫЦНУцжБНЧзјБъЯЕЃЈШчЭМЃЉЃЌЭМжаШ§ПщвѕгАВПЗжЕФУцЛ§ЗжБ№МЧЮЊS1ЁЂS2ЁЂS3ЃЌВЂВтЕУS2=6ЃЈЕЅЮЛЃКЦНЗНУзЃЉЃЎOG=GH=HIЃЎ
ЃЈ1ЃЉЧѓS1КЭS3ЕФжЕЃЛ
ЃЈ2ЃЉЩшTЃЈxЃЌyЃЉЪЧЭфЕРMNЩЯЕФШЮвЛЕуЃЌаДГіyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЙЋдАзМБИЖдЧјгђMPOQNФкВПНјааТЬЛЏИФдьЃЌдкКсзјБъЁЂзнзјБъЖМЪЧХМЪ§ЕФЕуДІжжжВЛЈФОЃЈЧјгђБпНчЩЯЕФЕуГ§ЭтЃЉЃЌвбжЊMP=2УзЃЌNQ=3УзЃЎЮЪвЛЙВФмжжжВЖрЩйПУЛЈФОЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com