
【题目】如图,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD= ![]() ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 ![]() ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( ) 
A.1
B.3﹣ ![]()
C.![]() ﹣1
﹣1
D.4﹣2 ![]()
【答案】D
【解析】解:如图,延长AE交BC的延长线于G, ∵E为CD中点,
∴CE=DE,
∵AD∥BC,
∴∠DAE=∠G=30°,
在△ADE和△GCE中,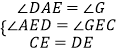 ,
,
∴△ADE≌△GCE(AAS),
∴CG=AD= ![]() ,AE=EG=2
,AE=EG=2 ![]() ,
,
∴AG=AE+EG=2 ![]() +2
+2 ![]() =4
=4 ![]() ,
,
∵AE⊥AF,
∴AF=AGtan30°=4 ![]() ×
× ![]() =4,
=4,
GF=AG÷cos30°=4 ![]() ÷
÷ ![]() =8,
=8,
过点A作AM⊥BC于M,过点D作DN⊥BC于N,
则MN=AD= ![]() ,
,
∵四边形ABCD为等腰梯形,
∴BM=CN,
∵MG=AGcos30°=4 ![]() ×
× ![]() =6,
=6,
∴CN=MG﹣MN﹣CG=6﹣ ![]() ﹣
﹣ ![]() =6﹣2
=6﹣2 ![]() ,
,
∵AF⊥AE,AM⊥BC,
∴∠FAM=∠G=30°,
∴FM=AFsin30°=4× ![]() =2,
=2,
∴BF=BM﹣MF=6﹣2 ![]() ﹣2=4﹣2
﹣2=4﹣2 ![]() .
.
故选:D.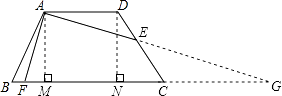
延长AE交BC的延长线于G,根据线段中点的定义可得CE=DE,根据两直线平行,内错角相等可得到∠DAE=∠G=30°,然后利用“角角边”证明△ADE和△GCE全等,根据全等三角形对应边相等可得CG=AD,AE=EG,然后解直角三角形求出AF、GF,过点A作AM⊥BC于M,过点D作DN⊥BC于N,根据等腰梯形的性质可得BM=CN,再解直角三角形求出MG,然后求出CN,MF,然后根据BF=BM﹣MF计算即可得解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在同一直角坐标系中,直线y=﹣x+3与y=3x﹣5相交于C点,分别与x轴交于A、B两点.P、Q分别为直线y=﹣x+3与y=3x﹣5上的点.
(1)求△ABC的面积;
(2)若P、Q关于原点成中心对称,求P点的坐标;
(3)若△QPC≌△ABC,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线y=﹣ ![]() x2+x+c与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
x2+x+c与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
(1)求此抛物线的解析式;
(2)①若点D是第一象限内抛物线上的一个动点,过点D作DE⊥x轴于E,连接CD,以OE为直径作⊙M,如图(2),试求当CD与⊙M相切时D点的坐标;
②点F是x轴上的动点,在抛物线上是否存在一点G,使A、C、G、F四点为顶点的四边形是平行四边形?若存在,求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况,所得数据用表格与条形图描述如下:
科目 | 语文 | 数学 | 英语 | 体育 | 音乐 |
人数 | 10 | a | 15 | 3 | 2 |

(1)表格中a的值为;
(2)补全条形图;
(3)小李是最喜欢体育之一,小张是最喜欢音乐之一,计划从最喜欢体育、音乐的人中,每科目各选1人参加学校训练,用列表或树形图表示所有结果,并求小李、小张至少有1人被选上的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
①bc>0;
②2a﹣3c<0;
③2a+b>0;
④ax2+bx+c=0有两个解x1 , x2 , 当x1>x2时,x1>0,x2<0;
⑤a+b+c>0;
⑥当x>1时,y随x增大而减小.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC, 
(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“爱心义卖”活动中,购进甲、乙两种文具,甲每个进货价高于乙进货价10元,90元买乙的数量与150元买甲的数量相同.
(1)求甲、乙进货价;
(2)甲、乙共100件,将进价提高20%进行销售,进货价少于2080元,销售额要大于2460元,求有几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)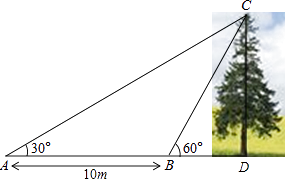
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )
A.1.2米
B.1.5米
C.1.9米
D.2.5米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com