
 如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.分析 (1)四种情况:当点M为AC的中点时,AM=BM;当点M与点C重合时,AB=BM;当点M在AC上,且AM=2时,AM=AB;当点M为CG的中点时,AM=BM;△ABM为等腰三角形;
(2)在AB上截取AK=AN,连接KN;由正方形的性质得出∠ADC=90°,AB=AD,∠CDG=90°,得出BK=DN,先证出∠BKN=∠NDH,再证出∠ABN=∠DNH,由ASA证明△BNK≌△NHD,得出BN=NH即可;
(3)①当M在AC上时,即0<t≤2$\sqrt{2}$时,△AMF为等腰直角三角形,得出AF=FM=$\frac{\sqrt{2}}{2}$t,求出S=$\frac{1}{2}$AF•FM=$\frac{1}{4}$t2;当t=2$\sqrt{2}$时,即可求出S的最大值;
②当M在CG上时,即2$\sqrt{2}$<t<4$\sqrt{2}$时,先证明△ACD≌△GCD,得出∠ACD=∠GCD=45°,求出∠ACM=90°,证出△MFG为等腰直角三角形,得出FG=MG•cos45°=4-$\frac{\sqrt{2}}{2}$t,得出S=S△ACG-S△CMJ-S△FMG.
解答 解:(1)点M为AC中点时,AM=BM,△ABM为等腰三角形
点M与点C重合时,AB=BM,△ABM为等腰三角形
点M为在AC上,且AM=2时,AB=AM,△ABM为等腰三角形
点M为CG中点时,AM=BM,△ABM为等腰三角形;
(2)(2)证明:在AB上截取AK=AN,连接KN;如图1所示: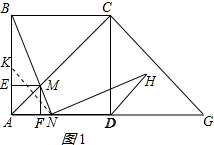 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴∠ADC=90°,AB=AD,
∴∠CDG=90°,
∵BK=AB-AK,ND=AD-AN,
∴BK=DN,
∵DH平分∠CDG,
∴∠CDH=45°,
∴∠NDH=90°+45°=135°,
∴∠BKN=180°-∠AKN=135°,
∴∠BKN=∠NDH,
在Rt△ABN中,∠ABN+∠ANB=90°,
又∵BN⊥NH,
即∠BNH=90°,
∴∠ANB+∠DNH=180°-∠BNH=90°,
∴∠ABN=∠DNH,
∴BNK≌△NHD(ASA),
∴BN=NH.
(3)①当点M在AC上时,即0<t≤2$\sqrt{2}$时,易知:△AMF为等腰直角三角形.
∵AM=t,∴AF=FM=$\frac{\sqrt{2}}{2}t$.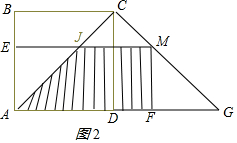
∴S=$\frac{1}{2}$AF•FM=$\frac{1}{2}$•$\frac{\sqrt{2}}{2}t$•$\frac{\sqrt{2}}{2}t$=$\frac{1}{4}$t2;
当点M在CG上时,即2$\sqrt{2}$<t<4$\sqrt{2}$时,CM=t-2$\sqrt{2}$,MG=4$\sqrt{2}$-t.
∵AD=DG,∠ADC=∠CDG,CD=CD,
∴△ACD≌△GCD(SAS),
∴∠ACD=∠GCD=45°
∴∠ACM=∠ACD+∠GCD=90°
∴∠G=90-∠GCD=90°-45°=45°
∴△MFG为等腰直角三角形.
∴FG=4-$\frac{\sqrt{2}}{2}t$,
∴S=S△ACG-S△ACJ-S△FMC=$\frac{1}{2}$×4×2-$\frac{1}{2}$×CM•CM-$\frac{1}{2}$FG•FM
=4-$\frac{1}{2}$(t-2$\sqrt{2}$)2-$\frac{1}{2}(4-\frac{\sqrt{2}}{2})^{2}$=-$\frac{3}{4}$t2+4$\sqrt{2}$t-8
∴S=$\left\{\begin{array}{l}{\frac{1}{4}{t}^{2}(0<t≤2\sqrt{2})}\\{-\frac{3}{4}{t}^{2}+4\sqrt{2}t-8(2\sqrt{2}<t<4\sqrt{2})}\end{array}\right.$.
点评 本题是相似形综合题目,考查了等腰三角形的判定、正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、三角函数以及三角形面积的计算等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,通过证明三角形全等和等腰直角三角形才能得出结果.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
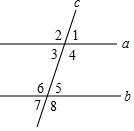 如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )
如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0),B(3,0).探究:抛物线y=x2-2mx+m2-4(m为常数)交x轴于点M,N两点;
如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0),B(3,0).探究:抛物线y=x2-2mx+m2-4(m为常数)交x轴于点M,N两点;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com