Question

3．将面积为4的正方形ABCD与面积为8的正方形AEFG按图①的位置放置，AD、AE在同一条直线上，AB、AG在同一条直线上．
（1）试判断DG、BE的数量和位置关系，并说明理由；
（2）如图2，将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，求此时BE的长．

Answer 1

分析 （1）由正方形的性质可证△ADG≌△ABE（SAS），因此可证得∠AGD=∠AEB，如图1，延长EB交DG于点H，然后由三角形的内角和和直角三角形的两锐角互余可证得结论；由正方形的性质和等量代换可证△ADG≌△ABE（SAS），因此可证得DG=BE，
（2）如图2，过点A作AM⊥DG交DG于点M，根据正方形的性质可证得DM=AM=$\sqrt{2}$，然后根据勾股定理可求得GM的长，进而可求得BE=DG=DM+GM．

解答 解：（1）如图1，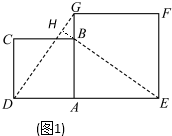

四边形ABCD与四边形AEFG是正方形，
∴AD=AB，∠DAG=∠BAE=90°，AG=AE，
∴△ADG≌△ABE（SAS），
∴∠AGD=∠AEB，
延长EB交DG于点H，
△ADG中∠AGD+∠ADG=90°，
∴∠AEB+∠ADG=90°，
△DEH中，∠AEB+∠ADG+∠DHE=180°，
∴∠DHE=90°，
∴DG⊥BE，
（2）四边形ABCD与四边形AEFG是正方形，
∴AD=AB，∠DAB=∠GAE=90°，AG=AE，
∴∠DAB+∠BAG=∠GAE+∠BAG，
∴∠DAG=∠BAE，
AD=AB，∠DAG=∠BAE，AG=AE，
∴△ADG≌△ABE（SAS），
∴DG=BE，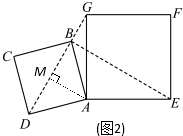

如图2，过点A作AM⊥DG交DG于点M，
∠AMD=∠AMG=90°
BD是正方形ABCD的对角线，
∴∠MDA=45°，
∵面积为4的正方形ABCD与面积为8的正方形AEFG
∴AD=2，AE=2$\sqrt{2}$，
在Rt△AMD中，∠MDA=45°，
∴COS45°=$\frac{DM}{AD}$，
∴DM=$\sqrt{2}$，
∴AM=$\sqrt{2}$，
在Rt△AMG中，GM=$\sqrt{A{G}^{2}-A{M}^{2}}$=$\sqrt{6}$，
∵DG=DM+GM=$\sqrt{2}$+$\sqrt{6}$，
∴BE=DG=$\sqrt{2}$+$\sqrt{6}$，

点评 此题主要考查了正方形的性质，锐角三角函数，全等三角形的性质和判定，解本题的关键是锐角三角函数的灵活运用．