
 某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.分析 作AH⊥CD于H,作CF⊥AB于F,在Rt△AHD中利用三角函数求得DH的长,在Rt△BCF中利用三角函数求得BF的长,则AB的长即可求得.
解答  解:作AH⊥CD于H,作CF⊥AB于F,
解:作AH⊥CD于H,作CF⊥AB于F,
在Rt△AHD中,∠ADH=37°,由sin37°=$\frac{AH}{AD}$,得AD=8.5(m),
由tan37°=$\frac{AH}{DH}$,得DH=$\frac{AH}{tan37°}$=$\frac{5.1}{\frac{3}{4}}$=6.8(m),
Rt△BCF中,∠CBF=45°,BF=CF=5.1m,
∵AB+BF=HD+DC,
∴AB=6.8+1.4-5.1=3.1(m).
点评 此题考查了解直角三角形的应用,解答本题的关键是构建直角三角形,将实际问题转化为数学模型,难度一般.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
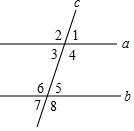 如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )
如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com