
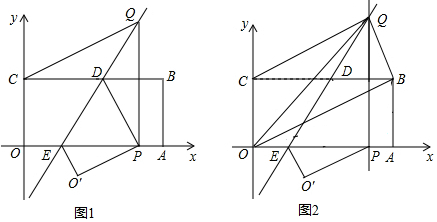
分析 (1)根据SAS证明△CDQ≌△PDQ,则CQ=PQ;
(2)根据Q(x,y)表示QH=y-2,CH=x,在Rt△CQH中,由勾股定理列式得:x2+(y-2)2=y2,化简可得结论,因为P在线段OA,且OA=4,又因为折痕所在直线与OA相交,即OP最小为2,所以2≤x≤4;
(3)先求直线OB的解析式为:y=$\frac{1}{2}$x,设直线OB与直线PQ相交于点G,设G(x,y),则Q(x,$\frac{1}{4}{x}^{2}$+1),
代入三角形面积公式计算S△OBQ的值,化简后得二次函数并配方,计算其最小值即可.
解答  解:(1)由折叠得:CD=PD,
解:(1)由折叠得:CD=PD,
∠CDE=∠PDE,
∴∠CDQ=∠PDQ,
又 DQ=DQ,
∴△CDQ≌△PDQ,
∴CQ=PQ;
(2)如图1,∵Q(x,y),
CQ=PQ=y,
∵B(4,2),
∴BC=4,AB=2,
设QP交BC于H,则QH=y-2,CH=x,
由勾股定理,得:x2+(y-2)2=y2,
∴y=$\frac{1}{4}{x}^{2}$+1(2≤x≤4);
(3)设直线OB的解析式为:y=kx,
把B(4,2)代入得:4k=2,
k=$\frac{1}{2}$,
∴直线OB的解析式为:y=$\frac{1}{2}$x,
设直线OB与直线PQ相交于点G,设G(x,y),
则Q(x,$\frac{1}{4}{x}^{2}$+1),
∴QG=$\frac{1}{4}{x}^{2}+1-\frac{1}{2}x$,
∴S△OBQ=$\frac{1}{2}$×4×($\frac{1}{4}{x}^{2}+1-\frac{1}{2}x$)=$\frac{1}{2}{x}^{2}-x+2$=$\frac{1}{2}$(x-1)2+$\frac{3}{2}$,
当x>1时,S随x的增大而增大,
∴当x=2时,S有最小值为2.
点评 本题是四边形的综合题,考查了矩形的性质、图形与坐标特点、二次函数的最值、三角形全等的性质和判定以及勾股定理,难度适中,第一问关键证明两三角形全等,第二问关键是确定一直角三角形利用勾股定理列方程得出结论,第三问根据不规则三角形的面积等于铅直高度与水平宽度的积的一半进行计算即可.


科目:初中数学 来源: 题型:解答题
 某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | (a+b)2-(a-b)2=4ab |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量y(百件) | y=-0.1x+8 | y=$\frac{120}{x}$ |
| 销售价格x(元/件) | 30≤x≤60 | 60<x≤80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
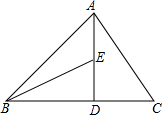 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.
如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com