
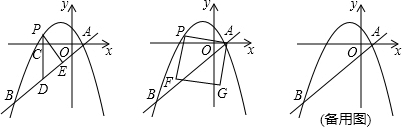
���� ��1������õ�A�͵�B�����꣬Ȼ��A�͵�B��������������ߵĽ���ʽ�����b��c��ֵ��
��2������֤����PDE�ס�AFO�ɵõ�PD��PE��DE=5��4��3�����P������Ϊ��x��-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$�������D������Ϊ��x��$\frac{3}{4}$x-$\frac{3}{2}$�����г�PD��x�ĺ�����ϵʽ�������PD�����ֵ�͵�P�����꣬Ȼ������m=PD+DE+PE�����m�����ֵ���ڵ���F��y����ʱ������A��AN��y�ᣬPN��x�ᣬPN��y�����M����֤����PAN�ա�FPM����AN=PM����P�ĺ���������ȣ��ݴ��г�����x�ķ�����⼴�ɣ�����G��y����ʱ������P��PN��x�ᣬ����ΪN����֤����PAN�ա�AOG���ɵõ�PN=OA=2���ʴ˿ɵõ���P��������Ϊ2����y=2���������ߵĽ���ʽ��ö�Ӧ��x��ֵ���ɣ�
��� �⣺��1����y=0����ֱ�ߵĽ���ʽ�ã�$\frac{3}{4}$x-$\frac{3}{2}$=0����ã�x=2��
���A��������2��0����
��x=-8����ֱ�ߵĽ���ʽ�ã�y=-$\frac{15}{7}$��
���B��������-8��-$\frac{15}{7}$����
����A�͵�B��������������ߵĽ���ʽ�ã�$\left\{\begin{array}{l}{-1+2b+c=0}\\{-16-8b+c=-\frac{15}{7}}\end{array}\right.$����ã�c=2.5��b=-$\frac{3}{4}$��
�������ߵĽ���ʽΪy=-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$��
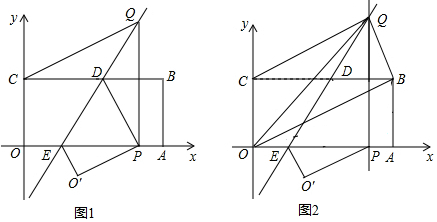
��2������ͼ1��ʾ��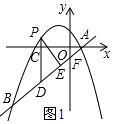
�߽�x=0����ֱ��AB�Ľ���ʽ�ã�y=-$\frac{3}{2}$��
��OF=$\frac{3}{2}$��
��Rt��OAF��AF=$\frac{5}{3}$��
��PD��y�ᣬ
���PDE=��OFA��
�֡ߡ�PED=��AOF��
���PDE�ס�AFO��
��PD��PE��DE=5��4��3��
���P��������x��-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$����
���D��������x��$\frac{3}{4}$x-$\frac{3}{2}$����PD=��-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$��-��$\frac{3}{4}$x-$\frac{3}{2}$��=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4=-$\frac{1}{4}$��x+3��2+$\frac{25}{4}$��
�൱x=-3ʱ��PD�ij��������ֵ�����ֵΪ$\frac{25}{4}$��
���P��������-3��$\frac{5}{2}$����
��m=PD+DE+PE��
��m=PD+$\frac{4}{5}$PD+$\frac{3}{5}$PD=$\frac{12}{5}$PD=$\frac{12}{5}$��$\frac{25}{4}$=15����m�����ֵΪ15��
����ͼ2��ʾ������F��y����ʱ������A��AN��y�ᣬPN��x�ᣬPN��y�����M��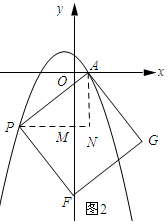
�ߡ�NPA+��FPM=90�㣬��NPA+��PAN=90�㣬
���FPM=��PAN��
�ڡ�PAN�͡�FPM��$\left\{\begin{array}{l}{��FPM=��PAN}\\{��PNA=��PMF}\\{PA=PF}\end{array}\right.$��
���PAN�ա�FPM��
��AN=PM��
���P��������x��-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$����
��AN=PM��
��x=-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$����ã�x=$\frac{-7+\sqrt{89}}{2}$��x=$\frac{-7-\sqrt{89}}{2}$����ȥ����
���P��������$\frac{-7+\sqrt{89}}{2}$��$\frac{-7+\sqrt{89}}{2}$����
��ͼ3��ʾ������G��y����ʱ������P��PN��x�ᣬ����ΪN��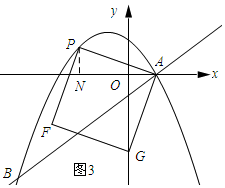
�ߡ�PAN+��NPA=90�㣬��PAN+��NAG=90�㣬
���NPA=��OAG��
�ڡ�PAN�͡�AOG��$\left\{\begin{array}{l}{��NPA=��OAG}\\{��PNA=��AOG}\\{PA=GA}\end{array}\right.$��
���PAN�ա�AOG��
��PN=OA=2��
��y=2���������ߵĽ���ʽ�ã�-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$=2����ã�x=$\frac{-3+\sqrt{17}}{2}$��x=$\frac{-3-\sqrt{17}}{2}$��
���P��������$\frac{-3+\sqrt{17}}{2}$��2����$\frac{-3-\sqrt{17}}{2}$��2����
������������P��������$\frac{-7+\sqrt{89}}{2}$��$\frac{-7+\sqrt{89}}{2}$����$\frac{-3+\sqrt{17}}{2}$��2����$\frac{-3-\sqrt{17}}{2}$��2����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ�����κ��������ʡ����������ε����ʺ��ж���ȫ�������ε����ʺ��ж����������⻭��ͼ�β�����ȫ�������ε����ʵõ���P�����������õ�P�ĺ�������֮��Ĺؼ��ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��1��0����B��3��0����̽����������y=x2-2mx+m2-4��mΪ��������x���ڵ�M��N���㣻
��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��1��0����B��3��0����̽����������y=x2-2mx+m2-4��mΪ��������x���ڵ�M��N���㣻�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
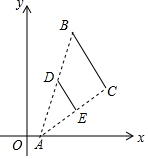 ��ͼ���߶�BC�����˵������ֱ�ΪB��3��7����C��6��3�����Ե�A��1��0��Ϊλ�����ģ����߶�BC��СΪԭ����$\frac{1}{2}$��õ��߶�DE����˵�D������Ϊ��������
��ͼ���߶�BC�����˵������ֱ�ΪB��3��7����C��6��3�����Ե�A��1��0��Ϊλ�����ģ����߶�BC��СΪԭ����$\frac{1}{2}$��õ��߶�DE����˵�D������Ϊ��������| A�� | ��1��$\frac{7}{2}$�� | B�� | ��2��$\frac{7}{2}$�� | C�� | ��1��2�� | D�� | ��2��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
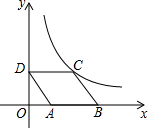 ��ͼ��?ABCD������ƽ��ֱ������ϵ�У���֪��A��2��0����B��6��0����D��0��3����������������ͼ����C����?ABCD����ƽ�ƣ�ʹ��Bǡ������˫�����ϣ���ʱA��B��C��D�Ķ�Ӧ��ֱ�ΪA�䣬B�䣬C�䣬D�䣬��C��D����˫���߽��ڵ�E�����E������Ϊ��$\frac{12}{5}$��5����
��ͼ��?ABCD������ƽ��ֱ������ϵ�У���֪��A��2��0����B��6��0����D��0��3����������������ͼ����C����?ABCD����ƽ�ƣ�ʹ��Bǡ������˫�����ϣ���ʱA��B��C��D�Ķ�Ӧ��ֱ�ΪA�䣬B�䣬C�䣬D�䣬��C��D����˫���߽��ڵ�E�����E������Ϊ��$\frac{12}{5}$��5�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a2•a=3a3 | B�� | ��2a��2��a=4a | C�� | ��-3a��2=3a2 | D�� | ��a-b��2=a2-b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
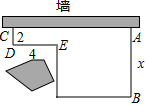 ��һ�γ�Ϊ32m������ƹ��ϰ���Χ��һ��������һ�߿�ǽ����ͼ����֪CD=2m��DE=4m����AB=x��m����2��x��14���������Ϊy��m2������ش��������⣺
��һ�γ�Ϊ32m������ƹ��ϰ���Χ��һ��������һ�߿�ǽ����ͼ����֪CD=2m��DE=4m����AB=x��m����2��x��14���������Ϊy��m2������ش��������⣺�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com