
 如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0),B(3,0).探究:抛物线y=x2-2mx+m2-4(m为常数)交x轴于点M,N两点;
如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0),B(3,0).探究:抛物线y=x2-2mx+m2-4(m为常数)交x轴于点M,N两点;分析 探究:(1)当m=2时,得到y=x2-4x=(x-2)2-4;于是得到结论;
(2)解方程x2-2mx+m2-4=0,得到x1=m+2,x2=m-2,.于是得到结论;②解方程x2-2mx+m2-4=0,得到交点坐标为M(m-2,0),N(m+2,0)解不等式即可得到结论;
拓展:(1)根据抛物线的解析式即可得到结论;
(2)解方程a2(x-b)2-4=0,得到x1=b-$\frac{2}{a}$=-$\frac{1}{a}$,x2=$\frac{3}{a}$,当该抛物线与线段AB有公共点时,与x轴的交点分别介于A,B之间,于是得到结论.
解答 解:探究:(1)当m=2时,y=x2-4x=(x-2)2-4;
∴抛物线的顶点坐标为(2,-4);
当y=0时,x2-4x=0,
解得:x1=0,x2=4,
∴线段MN的长为4;
(2)①线段MN的长度不发生改变,
理由:当y=0时,x2-2mx+m2-4=0,
解得:x1=m+2,x2=m-2,.
∴线段MN的长为4,
∴线段MN的长度不发生改变;
②令y=x2-2mx+m2-4=0,
解得:x1=m-2,x2=m+2,
即交点坐标为M(m-2,0),N(m+2,0)
当该抛物线与线段AB有公共点时,M,N分别介于A,B之间,
即1≤m-2≤3,1≤m+2≤3,
即∵m的取值范围是:-1≤m≤1,3≤m≤5;
拓展:
(1)该抛物线与y轴的交点坐标为(0,-3),…(10分)
(2)令y=a2(x-b)2-4=0,
解得:x1=b-$\frac{2}{a}$=-$\frac{1}{a}$,x2=$\frac{3}{a}$,
当该抛物线与线段AB有公共点时,与x轴的交点分别介于A,B之间,
1≤-$\frac{1}{a}$≤3,1≤$\frac{3}{a}$≤3,
a的取值范围是:-1≤a≤-$\frac{1}{3}$,1≤a≤3.
点评 本题考查了抛物线与x轴的交点,正确的理解题意列出方程是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 求不等式组$\left\{\begin{array}{l}{3x+3>5(x-1)①}\\{\frac{2x-2}{3}-1≤\frac{3x}{2}②}\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.
求不等式组$\left\{\begin{array}{l}{3x+3>5(x-1)①}\\{\frac{2x-2}{3}-1≤\frac{3x}{2}②}\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
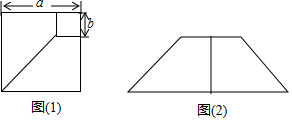
| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | (a+b)2-(a-b)2=4ab |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com