
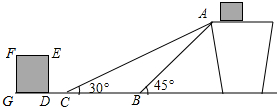
 如图,是某货运站传送货物的平面示意图.传送带AB长为4米,在离B点5米远的地方有一堆货物DEFG等待运输.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.但要保证货物着地点C的左侧留出2米的通道,试判断货物DEFG是否需要挪走.(结果精确到0.1米:参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24,$\sqrt{6}$≈2.45)
如图,是某货运站传送货物的平面示意图.传送带AB长为4米,在离B点5米远的地方有一堆货物DEFG等待运输.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.但要保证货物着地点C的左侧留出2米的通道,试判断货物DEFG是否需要挪走.(结果精确到0.1米:参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24,$\sqrt{6}$≈2.45) 分析 过A作AD⊥BC于D,在Rt△ABD中,根据特殊角的三角函数值求出AD,再根据在直角三角形中,30°所对的直角边等于斜边的一半求出AC,根据勾股定理求出CD,从而求出CB,最后根据DC=DB-CB求出DC,然后与2米进行比较,即可得出答案.
解答 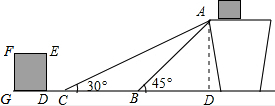 解:如图,作AD⊥BC于点D;
解:如图,作AD⊥BC于点D;
在Rt△ABD中,
AD=BD=ABsin45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$,
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=4$\sqrt{2}$;
在Rt△ACD中,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{(4\sqrt{2})^{2}-(2{\sqrt{2})}^{2}}$=2$\sqrt{6}$;
∴CB=CD-BD=2$\sqrt{6}$-2$\sqrt{2}$≈2.1.
∵DC=DB-CB≈5-2.1=2.9>2;
∴货物DEFG不需要挪走.
点评 此题考查的是解直角三角形的应用,在两个直角三角形拥有公共边的情况下,先求出这条公共边是解答此类题目的关键.


 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源: 题型:选择题
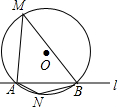 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 17 | C. | 9 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
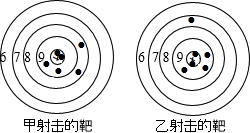 如图是甲乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.
如图是甲乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com