
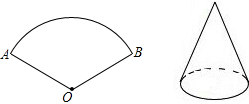
 如图,将弧长为6π,圆心角为120°的圆形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是6$\sqrt{2}$.
如图,将弧长为6π,圆心角为120°的圆形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是6$\sqrt{2}$. 科目:初中数学 来源: 题型:解答题
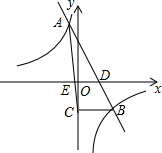 一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A(-1,4),B(2,n)两点,直线AB交x轴于点D.
一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A(-1,4),B(2,n)两点,直线AB交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
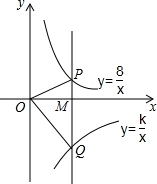 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=$\frac{8}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象交于P、Q两点,若S△POQ=14,则k的值为-20.
如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=$\frac{8}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象交于P、Q两点,若S△POQ=14,则k的值为-20.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 两人相遇次数(单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和(单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
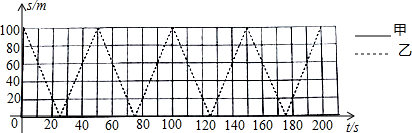
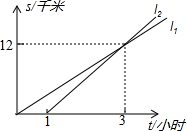 A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/小时;④乙先到达B地.其中正确的个数是( )
A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/小时;④乙先到达B地.其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.49×107 | B. | 7.49×106 | C. | 74.9×105 | D. | 0.749×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC=12cm.
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC=12cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x+4=9 | B. | $\frac{1}{x}+\frac{2}{3y}=2$ | C. | x2+y=0 | D. | 6x+1=y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com