
【题目】如图1,在![]() 中,
中,![]() 是BC上的一点,以AD为边作
是BC上的一点,以AD为边作![]() ,使
,使![]() .
.
(1)直接用含![]() 的式子表示
的式子表示![]() 的度数是_______________;
的度数是_______________;
(2)以![]() 为边作平行四边形
为边作平行四边形![]() ;
;
①如图2,若点F恰好落在DE上,试判断线段BD与线段CD的长度是否相等,并说明理由.
②如图3,若点F落在是DE上,且![]() ,求线段CF的长(直接写出结果,不说明理由).
,求线段CF的长(直接写出结果,不说明理由).

【答案】(1)![]() ;(2)①相等,见解析,②
;(2)①相等,见解析,②![]()
【解析】
(1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
(1)∵在△ABC中,AB=AC,∠ABC=α,
∴∠BAC=180°2α,
∵∠DAE+∠BAC=180°,
∴∠DAE=2α,
∵AE=AD,
∴∠ADE=90°α;
故答案为:90°α;
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥EF.
∴∠EDC=∠ABC=α,
由(1)知,∠ADE=90°α,
∴∠ADC=∠ADE+∠EDC=90°,
∴AD⊥BC.
∵AB=AC,
∴BD=CD;
②证明:∵AB=AC,∠ABC=α,
∴∠C=∠B=α.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴∠EAC=∠C=α,
由(1)知,∠DAE=2α,
∴∠DAC=α,
∴∠DAC=∠C.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
∴![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与
与 ![]() 轴的一个交点A在点(-2,0)和(1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则
轴的一个交点A在点(-2,0)和(1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则 ![]() 的取值范围是 .
的取值范围是 . 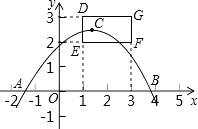
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
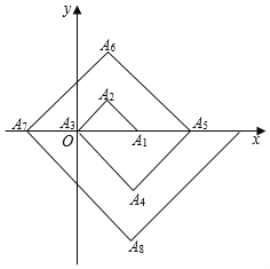
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
科目:初中数学 来源: 题型:
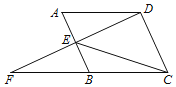
【题目】如图,平行四边形![]() 中,点E是边AB的中点,延长DE交CB的延长线于点F.
中,点E是边AB的中点,延长DE交CB的延长线于点F.
(1)求证:![]() ;
;
(2)若![]() ,连接EC,则
,连接EC,则![]() 的度数是__________________
的度数是__________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“科学”号是我国目前最先进的海洋科学综合考察船,它在南海利用探测仪在海面下方探测到点C处有古代沉船.如图,海面上两探测点A,B相距1400米,探测线与海面的夹角分别是30°和60°.试确定古代沉船所在点C的深度.(结果精确到1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2( ),
且∠1=∠4( )
∴∠2=∠4(等量代换)
∴CE∥BF( )
∴∠ =∠3( )
又∵∠B=∠C(已知)
∴∠3=∠B( )
∴AB∥CD( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三对某班最近一次数学测验成绩(得分取整数)进行统计分析,将所有成绩由低到高分成五组,并绘制成如图的频数分布直方图,请结合直方图提供的信息,回答下列问题:
(1)该班共有______名同学参加这次测验;
(2)这次测验成绩的中位数落在______分数段内;
(3)若该校一共有800名初三学生参加这次测验,成绩80分以上(不含80分)为优秀,估计该校这次数学测验的优秀人数是多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com