
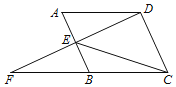
【题目】如图,平行四边形![]() 中,点E是边AB的中点,延长DE交CB的延长线于点F.
中,点E是边AB的中点,延长DE交CB的延长线于点F.
(1)求证:![]() ;
;
(2)若![]() ,连接EC,则
,连接EC,则![]() 的度数是__________________
的度数是__________________
【答案】(1)见解析;(2)![]()
【解析】
(1)由平行四边形的性质得出AD∥BC,得出∠A=∠ABF,由ASA证明△ADE≌△BFE即可;
(2)由全等三角形的性质得出DE=EF,由平行四边形的性质得出AB∥DC,AB=CD,得出∠CDF=∠BEF,证出∠CDF=90°,DE=DC,由等腰直角三角形的性质得出∠DEC=∠DCE=45°,即可得出结果.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A=∠ABF,
∵点E是AB的中点,
∴AE=BE,
在△ADE和△BFE中,
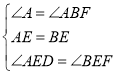 ,
,
∴△ADE≌△BFE(ASA);
(2)解:∵△ADE≌△BFE,
∴DE=EF,
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∴∠CDF=∠BEF
∵DE⊥AB,
∴∠BEF=90°,
∴∠CDF=90°,
∵DE=AB,
∴DE=DC,
∴△DCE是等腰直角三角形,
∴∠DEC=∠DCE=45°,
∴∠FEC=135°.
故答案为:135°.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.若AC=6,AB=10,则⊙O的半径为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC=20cm,BC=16cm,D为AB中点,如果点P在线段BC上由点B出发向点C运动,同时点Q在线段CA上由点C出发向点A运动,设运动时间为t(s).
(1)若点P与点Q的速度都是2cm/s,问经过多少时间△BPD与△CQP全等?说明理由;
(2)若点P的速度比点Q的速度都慢2cm/s,则经过多少时间△BPD与△CQP全等,并求出此时两点的速度;
(3)若点P、点Q分别以(2)中速度同时从B、C出发,都逆时针沿△ABC三边运动,问经过多少时间点P与点Q第一次相遇,相遇点在△ABC的哪条边上?并求出相遇点与点B的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,点P从点A出发,沿A→B→C以1cm/s的速度运动.设△APC的面积为s(m),点P的运动时间为t(s),变量S与t之间的关系如图2所示,则在运动过程中,S的最大值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 是BC上的一点,以AD为边作
是BC上的一点,以AD为边作![]() ,使
,使![]() .
.
(1)直接用含![]() 的式子表示
的式子表示![]() 的度数是_______________;
的度数是_______________;
(2)以![]() 为边作平行四边形
为边作平行四边形![]() ;
;
①如图2,若点F恰好落在DE上,试判断线段BD与线段CD的长度是否相等,并说明理由.
②如图3,若点F落在是DE上,且![]() ,求线段CF的长(直接写出结果,不说明理由).
,求线段CF的长(直接写出结果,不说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动.
(1)四边形DEBF是平行四边形吗?说明你的理由.
(2)若BD=10cm,AC=18cm,当运动时间t为多少时,四边形DEBF为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式及其验证过程:
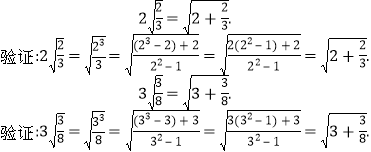
![]() 按照上述两个等式及其验证过程的基本思路,猜想
按照上述两个等式及其验证过程的基本思路,猜想![]() 的变形结果并进行验证;
的变形结果并进行验证;
![]() 针对上述各式反应的规律,写出用
针对上述各式反应的规律,写出用![]() 为任意自然数,且
为任意自然数,且![]() 表示的等式,并说明它成立.
表示的等式,并说明它成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com