
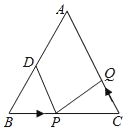
����Ŀ����ͼ��ʾ���ڡ�ABC�У�AB��AC��20cm��BC��16cm��DΪAB�е㣬�����P���߶�BC���ɵ�B�������C�˶���ͬʱ��Q���߶�CA���ɵ�C�������A�˶������˶�ʱ��Ϊt��s����
��1������P���Q���ٶȶ���2cm/s���ʾ�������ʱ���BPD���CQPȫ�ȣ�˵�����ɣ�
��2������P���ٶȱȵ�Q���ٶȶ���2cm/s��������ʱ���BPD���CQPȫ�ȣ��������ʱ������ٶȣ�
��3������P����Q�ֱ��ԣ�2�����ٶ�ͬʱ��B��C����������ʱ���ء�ABC�����˶����ʾ�������ʱ���P���Q��һ���������������ڡ�ABC���������ϣ���������������B�ľ��룮

���𰸡���1������3s��BPD���CQPȫ�ȣ���2�����˶�ʱ��Ϊ1sʱ����BPD���CPQȫ�ȣ���ʱ��P���ٶ�Ϊ8cm/s����Q���ٶ�Ϊ10cm/s����3����һ��������AB���ϣ���ʱ���������B�ľ���8cm��
��������
��1�����ݵ��������ε����ʿɵó���B����C���ɵ�P��Qͬ��ͬʱ�����ɵó�BP��CQ�����ȫ�������ε��ж������ɵó���BD��CPʱ��BPD���CQPȫ�ȣ��������ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��2�����P���ٶ�Ϊxcm/s�����Q���ٶ�Ϊ��x+2��cm/s����BP��CQ����B����C���ȫ�������ε����ʿɵó�BD��CQ��BP��CP��8���������ɵó�����t��x�ķ����飬��֮���ɵó����ۣ�
��3������·�̣��ٶȡ�ʱ���ϵ�P��Q���������ɵó�����t��һԪһ�η��̣���֮�����tֵ���ɵ�Q��·�̣���Q���ٶȡ��˶�ʱ��������Q��·�̣��ٽ��CA��AB��BC�ij��ȣ������ҳ���P��Q��һ������ʱ��λ�ã�����ý⣮
�⣺��1����AB��AC��
���B����C��
�ߵ�P���Q���ٶȶ���2cm/s��
��BP��CQ��
�൱BD��CPʱ����BPD���CQPȫ�ȣ���10��16��2t��
���t��3��
�ྭ��3s��BPD���CQPȫ�ȣ�
��2�����P���ٶ�Ϊxcm/s�����Q���ٶ�Ϊ��x+2��cm/s��
��BP��CQ����B����C��
��BD��CQ��BP��CP��8��
��![]() ��
��
��ã�![]() ��
��
�൱�˶�ʱ��Ϊ1sʱ����BPD���CPQȫ�ȣ���ʱ��P���ٶ�Ϊ8cm/s����Q���ٶ�Ϊ10cm/s��
��3����������ã�10t��40+8t��
��ã�t��20��
��Q��·�̣�10��20��200��cm����
��200����20+20+16����3+20+12��20��12��8��
���һ��������AB���ϣ���ʱ���������B�ľ���8cm��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
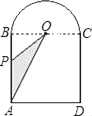
����Ŀ����ͼ��һ����������ABCD�Ͱ�ԲO��ɵķ��ͼ�Σ���O��Բ�ģ���P�ӵ�A���������߶�AB����BC���߶�CD�����˶��������յ�D���˶�������OPɨ���������s����ʱ�䣨t���仯��ͼ������ǣ�������
A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ����8000Ԫ����һ����������58Ԫ/���ļ۸���ۣ��ܿ����꣬Ȼ������17600Ԫ����ͬ����������������ǵ�һ�ε�2���������ĵ��۱���һ��ÿ����4Ԫ����װ����ԭ�ۼ�58Ԫ/�����ۣ�����ȫ�����꣮
��1���÷�װ���һ�ι����������ټ���
��2�����÷�װ�����ι�����������һ�����⣬��ô���������ӯ�����ǿ������ӯ��������𣩶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У�![]() ƽ��
ƽ��![]() ���ҡ�ACB=40�㣬��BAC=70�㣮
���ҡ�ACB=40�㣬��BAC=70�㣮
��1��AD��BCƽ������д���������̣�
��2����![]() ��
��![]() �Ķ�����
�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����������ӵ�һ����һ��ׯC���ӱ�ԭ������ȡˮ��A��B������AB��AC������ij��ԭ����C��A��·�����Ѿ���ͨ��ij��Ϊ�������ȡˮ�����ںӱ��½�һ��ȡˮ��H��A��H��B��һ��ֱ���ϣ���������һ��·CH�����CB��3ǧ�ף�CH��2.4ǧ�ף�HB��1.8ǧ�ף�
��1����CH�Ƿ�Ϊ�Ӵ�ׯC���ӱߵ����·�������ʣ�CH��AB�Ƿ�ֱ������ͨ���������˵����
��2����ԭ����·��AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�Ȼ�����������⣮
����֪������2x+3y=12��������⣬����ʵ����������������ֻ��Ҫ������������⣮������2x+3y=12����![]() ����x��yΪ����������
����x��y����������![]() ����0��x��6����
����0��x��6����![]() ����������
����������![]() ��������
��������
��2��3���ʣ���֪��xΪ3�ı������Ӷ�x=3������![]() ��
��
��2x+3y=12����������Ϊ![]()
���⣺
��1������д������2x+y=5��һ���������⣺______��
��2����![]() Ϊ��Ȼ����������������xֵ��______����
Ϊ��Ȼ����������������xֵ��______����
A��2B��3C��4D��5
��3�����꼶ij��Ϊ�˽���ѧϰ������ѧ���������˵���Ϊ3Ԫ�ıʼDZ��뵥��Ϊ5Ԫ�ĸֱ����ֽ�Ʒ��������35Ԫ�����м��ֹ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
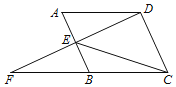
����Ŀ����ͼ��ƽ���ı���![]() �У���E�DZ�AB���е㣬�ӳ�DE��CB���ӳ����ڵ�F��
�У���E�DZ�AB���е㣬�ӳ�DE��CB���ӳ����ڵ�F��
��1����֤��![]() ��
��
��2����![]() ������EC����
������EC����![]() �Ķ�����__________________
�Ķ�����__________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȤС���о��ҹ��Ŵ����㷨ͳ�ڡ�������һ��ʫ�����ʿ������������ڿͶ��������У�һ���߿Ͷ��߿ͣ�һ���ſ�һ���գ�ʫ�к��������˼�ǣ����ÿһ��ͷ�ס7�ˣ���ô��7������ס�����ÿһ��ͷ�ס9�ˣ���ô�Ϳճ�һ�䷿��
��1����õ��пͷ����ټ䣿���Ͷ����ˣ�
��2������������������ͷ����и��������������ӣ�ÿ��ͷ��շ�20Ǯ����ÿ��ͷ������ס4�ˣ�һ���Զ��ͷ�18�����ϣ���18�䣩�����Ѱ�8���Żݣ���ʫ�С��ڿ͡��ٴ�һ����ס��������ζ��������㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com