
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() .
.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若![]() 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;
A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
【答案】(1)当x=1时,y=3;当x=2时,y=1(2)C(3)有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;或购买单价为3元的笔记本10本,单价为5元的钢笔1支.
【解析】
根据题意可知,求方程的正整数解,先把方程做适当的变形,再列举正整数代入求解.(1)(2)参照例题的解题思路进行解答;
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.则根据题意得:3m+5n=35,其中m、n均为自然数.参照例题的解题思路解该二元一次方程即可.
解:(1)由2x+y=5,得y=5-2x(x、y为正整数).
所以![]() ,即0<x<
,即0<x<![]()
∴当x=1时,y=3;
当x=2时,y=1.
即方程的正整数解是![]() 或
或![]() ;
;
(2)同样,若![]() 为自然数,
为自然数,
则有:0<x-2≤6,即2<x≤8.
当x=3时,![]() ;
;
当x=4时,![]() ;
;
当x=5时,![]() ;
;
当x=8时,![]() .
.
即满足条件x的值有4个,
故选C;
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.
则根据题意得:3m+5n=35,其中m、n均为自然数.
于是有:![]() ,
,
解得: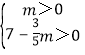 ,
,
所以0<m<![]() .
.
由于n=7-![]() m为正整数,则
m为正整数,则![]() m为正整数,可知m为5的倍数.
m为正整数,可知m为5的倍数.
∴当m=5时,n=4;
当m=10时,n=1.
答:有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;
或购买单价为3元的笔记本10本,单价为5元的钢笔1支.
故答案为:(1)当x=1时,y=3;当x=2时,y=1;(2)C;(3)有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;或购买单价为3元的笔记本10本,单价为5元的钢笔1支.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,海中有一灯塔P,它的周围8海里内有暗礁.海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线 ![]() 与抛物线
与抛物线 ![]() 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.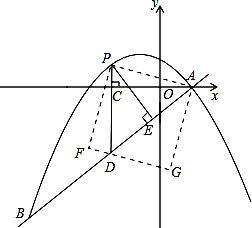
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为 ![]() ,点P的横坐标为
,点P的横坐标为 ![]() ,求
,求 ![]() 关于
关于 ![]() 的函数关系式,并求出
的函数关系式,并求出 ![]() 的最大值;
的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在 ![]() 轴上时,求出对应点P的坐标.
轴上时,求出对应点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC=20cm,BC=16cm,D为AB中点,如果点P在线段BC上由点B出发向点C运动,同时点Q在线段CA上由点C出发向点A运动,设运动时间为t(s).
(1)若点P与点Q的速度都是2cm/s,问经过多少时间△BPD与△CQP全等?说明理由;
(2)若点P的速度比点Q的速度都慢2cm/s,则经过多少时间△BPD与△CQP全等,并求出此时两点的速度;
(3)若点P、点Q分别以(2)中速度同时从B、C出发,都逆时针沿△ABC三边运动,问经过多少时间点P与点Q第一次相遇,相遇点在△ABC的哪条边上?并求出相遇点与点B的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“元旦”期间,平价商场对该商场商品进行如下的优惠促销活动:
打折前一次性购物总金额 | 优惠措施 |
小于等于 400 元 | 不优惠 |
超过 400 元,但不超过 600元 | 按售价打九折 |
超过 600 元 | 其中 600 元部分八折优惠,超过 600 元的部分打六折优惠 |
按上述优惠条件,若小华一次性购买售价为 80 元/件的商品 n 件时,实际付款 504 元, 则 n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,点P从点A出发,沿A→B→C以1cm/s的速度运动.设△APC的面积为s(m),点P的运动时间为t(s),变量S与t之间的关系如图2所示,则在运动过程中,S的最大值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com