
【题目】己知![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上一点,
上一点,![]() .
.
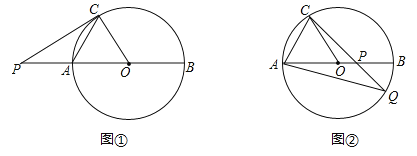
(Ⅰ)如图①,过点![]() 作
作![]() 的切线,与
的切线,与![]() 的延长线交于点
的延长线交于点![]() ,求
,求![]() 的大小;
的大小;
(Ⅱ)如图②,![]() 为
为![]() 上一点,
上一点,![]() 延长线与
延长线与![]() 交于点
交于点![]() .若
.若![]() ,求
,求![]() 的大小.
的大小.
【答案】(I)26![]() (II)48
(II)48![]()
【解析】
(I)根据等腰三角形中有一底角为58度时,可得∠COA=64![]() ,根据切线的性质得出∠OCP=90
,根据切线的性质得出∠OCP=90![]() ,进而求得∠P的度数;
,进而求得∠P的度数;
(II)先由(I)知∠AOC=64![]() ,根据圆周角定理得∠Q=
,根据圆周角定理得∠Q=![]() ∠AOC=32
∠AOC=32![]() ,根据等腰三角形的性质和三角形内角和定理得∠QAC=∠QCA=74
,根据等腰三角形的性质和三角形内角和定理得∠QAC=∠QCA=74![]() ,最后由三角形外角的性质可得结论.
,最后由三角形外角的性质可得结论.
(I)∵OA=OC,∠OAC=58![]() ,
,
∴∠OCA=58![]()
∴∠COA=180![]() 2×58
2×58![]() =64
=64![]()
∵PC是⊙O的切线,
∴∠OCP=90![]() ,
,
∴∠P=90![]() 64
64![]() =26
=26![]() ;
;
(II)∵∠AOC=64![]() ,
,
∴∠Q=![]() ∠AOC=32
∠AOC=32![]() ,
,
∵AQ=CQ,
∴∠QAC=∠QCA=74![]() ,
,
∵∠OCA=58![]() ,
,
∴∠PCO=74![]() 58
58![]() =16
=16![]() ,
,
∵∠AOC=∠QCO+∠APC,
∴∠APC=64![]() 16
16![]() =48
=48![]() .
.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】4张相同的卡片上分别写有数字-1、-3、4、6,将卡片的背面朝上,并洗匀.
(1)从中任意抽取1张,抽到的数字是奇数的概率是 ;
(2)从中任意抽取1张,并将所取卡片上的数字记作一次函数![]() 中的
中的![]() ;再从余下的卡片中任意抽取1张,并将所取卡片上的数字记作一次函数
;再从余下的卡片中任意抽取1张,并将所取卡片上的数字记作一次函数![]() 中的
中的![]() .利用画树状图或列表的方法,求这个一次函数的图象经过第一、二、四象限的概率.
.利用画树状图或列表的方法,求这个一次函数的图象经过第一、二、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
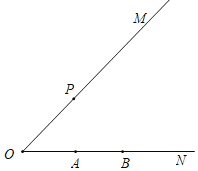
【题目】∠MON=45°,点P在射线OM上,点A,B在射线ON上(点B与点O在点A的两侧),且AB=1,以点P为旋转中心,将线段AB逆时针旋转90°,得到线段CD(点C与点A对应,点D与点B对应).
(1)如图,若OA=1,OP![]() ,依题意补全图形;
,依题意补全图形;
(2)若OP![]() ,当线段AB在射线ON上运动时,线段CD与射线OM有公共点,求OA的取值范围;
,当线段AB在射线ON上运动时,线段CD与射线OM有公共点,求OA的取值范围;
(3)一条线段上所有的点都在一个圆的圆内或圆上,称这个圆为这条线段的覆盖圆.若OA=1,当点P在射线OM上运动时,以射线OM上一点Q为圆心作线段CD的覆盖圆,直接写出当线段CD的覆盖圆的直径取得最小值时OP和OQ的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和
和![]() .下列结论:
.下列结论:
①![]() ;
;
②![]() ;
;
③当![]() 时,抛物线与
时,抛物线与![]() 轴必有一个交点在点
轴必有一个交点在点![]() 的右侧;
的右侧;
④抛物线的对称轴为![]() .
.
其中结论正确的个数有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)经过点(1,1)和(﹣1,0).下列结论:①a+c=1;②b2﹣4ac≥0;③当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧;④抛物线的对称轴为x=﹣![]() .其中结论正确的个数有( )
.其中结论正确的个数有( )
A.4 个B.3 个C.2 个D.1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当![]() ≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
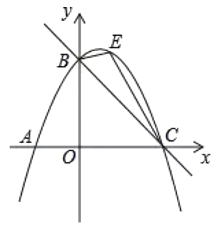
【题目】如图,直线![]() 与 x 轴交于点 C,与 y 轴交于点 B,抛物线
与 x 轴交于点 C,与 y 轴交于点 B,抛物线 ![]() 经过 B、C 两点.
经过 B、C 两点.
(1)求抛物线的解析式;
(2)如图,点 E 是抛物线上的一动点(不与 B,C 两点重合),△BEC 面积记为 S,当 S 取何值时,对应的点 E 有且只有三个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com