
【题目】4张相同的卡片上分别写有数字-1、-3、4、6,将卡片的背面朝上,并洗匀.
(1)从中任意抽取1张,抽到的数字是奇数的概率是 ;
(2)从中任意抽取1张,并将所取卡片上的数字记作一次函数![]() 中的
中的![]() ;再从余下的卡片中任意抽取1张,并将所取卡片上的数字记作一次函数
;再从余下的卡片中任意抽取1张,并将所取卡片上的数字记作一次函数![]() 中的
中的![]() .利用画树状图或列表的方法,求这个一次函数的图象经过第一、二、四象限的概率.
.利用画树状图或列表的方法,求这个一次函数的图象经过第一、二、四象限的概率.
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 匀速运动,当其中一点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一点到达终点时,另一个点也随之停止运动.设点![]() 、
、![]() 运动的时间是
运动的时间是![]() 秒
秒![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?若能,求出
能够成为菱形吗?若能,求出![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(3)当![]() ________时,
________时,![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x+2交x轴于点A,交y轴于点B,
x+2交x轴于点A,交y轴于点B,
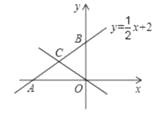
(1)求A,B两点的坐标;
(2)已知点C是线段AB上的一点,当S△AOC= ![]() S△AOB时,求直线OC的解析式。
S△AOB时,求直线OC的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一组数据2,2,3,4,这组数据的中位数是2
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D. 某日最高气温是![]() ,最低气温是
,最低气温是![]() ,则该日气温的极差是
,则该日气温的极差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏省第十九届运动会将于2018年9月在扬州举行开幕式,某校为了了解学生“最喜爱的省运会项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”、“游泳”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的省运会项目的人数调查统计表


根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 ,![]() ;
;
(2)扇形统计图中“自行车”对应的扇形的圆心角为 度;
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径作半圆,交
为半径作半圆,交![]() 于点
于点![]() .
.
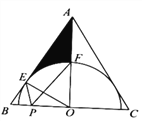
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若点![]() 是
是![]() 的中点,
的中点,![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)在(2)的条件下,点![]() 是
是![]() 边上的动点,当
边上的动点,当![]() 取最小值时,直接写出
取最小值时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位长度的速度向点
以每秒2个单位长度的速度向点![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时运动停止.设运动时间为
重合时运动停止.设运动时间为![]() 秒.
秒.
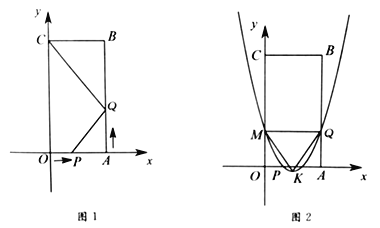
(1)当![]() 时,线段
时,线段![]() 的中点坐标为________;
的中点坐标为________;
(2)当![]() 与
与![]() 相似时,求
相似时,求![]() 的值;
的值;
(3)当![]() 时,抛物线
时,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,如图2所示.问该抛物线上是否存在点
,如图2所示.问该抛物线上是否存在点![]() ,使
,使![]() ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与实践
在学习完整式的乘除后,学习小组的组长小明同学准备利用长方形与正方形的面积间的关系来了解本组同学对所学知识的掌握情况.他给出的题目如下:在一个长![]() 厘米,宽
厘米,宽![]() 厘米的长方形
厘米的长方形![]() 内(
内(![]() ),将两张边长分别为
),将两张边长分别为![]() 厘米和
厘米和![]() 厘米(
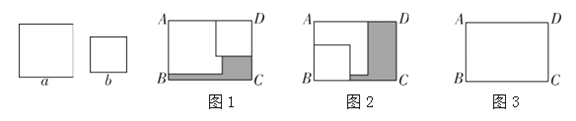
厘米(![]() )的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为
)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为![]() ,图2中阴影部分的面积为
,图2中阴影部分的面积为![]() .
.
(1)请你用m,n,a,b![]() 的代数式分别表示
的代数式分别表示![]() 和
和![]() ;
;
(2)当![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)仿照图1和图2,在图3中画出你按某种方式将边长分别为a厘米和b厘米的正方形纸片放置在长方形ABCD内的图案,长方形中未被两张正方形纸片覆盖的部分用斜线画出(即阴影部分),设新图形中阴影部分面积为![]() ,请用含m,n,a,b的代数式直接写出
,请用含m,n,a,b的代数式直接写出![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com