
【题目】如图1,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位长度的速度向点
以每秒2个单位长度的速度向点![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时运动停止.设运动时间为
重合时运动停止.设运动时间为![]() 秒.
秒.
(1)当![]() 时,线段
时,线段![]() 的中点坐标为________;
的中点坐标为________;
(2)当![]() 与
与![]() 相似时,求
相似时,求![]() 的值;
的值;
(3)当![]() 时,抛物线
时,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,如图2所示.问该抛物线上是否存在点
,如图2所示.问该抛物线上是否存在点![]() ,使
,使![]() ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
【答案】(1)![]() 的中点坐标是
的中点坐标是![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】(1)先根据时间t=2,和速度可得动点P和Q的路程OP和AQ的长,再根据中点坐标公式可得结论;
(2)根据矩形的性质得:∠B=∠PAQ=90°,所以当△CBQ与△PAQ相似时,存在两种情况:
①当△PAQ∽△QBC时,![]() ,②当△PAQ∽△CBQ时,
,②当△PAQ∽△CBQ时,![]() ,分别列方程可得t的值;
,分别列方程可得t的值;
(3)根据t=1求抛物线的解析式,根据Q(3,2),M(0,2),可得MQ∥x轴,∴KM=KQ,KE⊥MQ,画出符合条件的点D,证明△KEQ∽△QMH,列比例式可得点D的坐标,同理根据对称可得另一个点D.
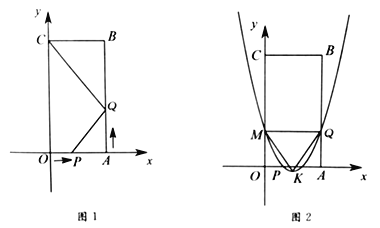
(1)如图1,∵点A的坐标为(3,0),
∴OA=3,
当t=2时,OP=t=2,AQ=2t=4,
∴P(2,0),Q(3,4),
∴线段PQ的中点坐标为:(![]() ,
,![]() ),即(
),即(![]() ,2);
,2);
故答案为:(![]() ,2);
,2);
(2)如图1,∵四边形OABC是矩形,
∴∠B=∠PAQ=90°
∴当△CBQ与△PAQ相似时,存在两种情况:
①当△PAQ∽△QBC时,![]() ,
,
∴![]() ,
,
4t2-15t+9=0,
(t-3)(t-![]() )=0,
)=0,
t1=3(舍),t2=![]() ,
,
②当△PAQ∽△CBQ时,![]() ,
,
∴![]() ,
,
t2-9t+9=0,
t=![]() ,
,
∵0≤t≤6,![]() >7,
>7,
∴x=![]() 不符合题意,舍去,
不符合题意,舍去,
综上所述,当△CBQ与△PAQ相似时,t的值是![]() 或
或![]() ;
;
(3)当t=1时,P(1,0),Q(3,2),
把P(1,0),Q(3,2)代入抛物线y=x2+bx+c中得:
![]() ,解得:
,解得:![]() ,
,
∴抛物线:y=x2-3x+2=(x-![]() )2-
)2-![]() ,
,
∴顶点k(![]() ,-
,-![]() ),
),
∵Q(3,2),M(0,2),
∴MQ∥x轴,
作抛物线对称轴,交MQ于E,
∴KM=KQ,KE⊥MQ,
∴∠MKE=∠QKE=![]() ∠MKQ,
∠MKQ,
如图2,∠MQD=![]() ∠MKQ=∠QKE,设DQ交y轴于H,
∠MKQ=∠QKE,设DQ交y轴于H,
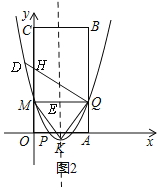
∵∠HMQ=∠QEK=90°,
∴△KEQ∽△QMH,
∴![]() ,
,
∴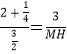 ,
,
∴MH=2,
∴H(0,4),
易得HQ的解析式为:y=-![]() x+4,
x+4,
则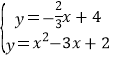 ,
,
x2-3x+2=-![]() x+4,
x+4,
解得:x1=3(舍),x2=-![]() ,
,
∴D(-![]() ,
,![]() );
);
同理,在M的下方,y轴上存在点H,如图3,使∠HQM=![]() ∠MKQ=∠QKE,
∠MKQ=∠QKE,
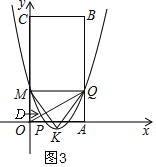
由对称性得:H(0,0),
易得OQ的解析式:y=![]() x,
x,
则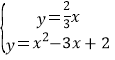 ,
,
x2-3x+2=![]() x,
x,
解得:x1=3(舍),x2=![]() ,
,
∴D(![]() ,
,![]() );
);
综上所述,点D的坐标为:D(-![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】某商店出售网球和网球拍,网球拍每只定价80元,网球每个定价4元,商家为促销商品,同时向客户提供两种优惠方案:①买一只网球拍送3个网球:②网球拍和网球都按定价的9折优惠,现在某客户要到该商店购买球拍20只,网球![]() 个(
个(![]() 大于20).
大于20).
(1)若该客户按优惠方案①购买需付款多少元?(用含![]() 的式子表示)
的式子表示)
(2)若该客户按优惠方案②购买需付款多少元?(用含![]() 的式子表示)
的式子表示)
(3)若![]() 时,通过计算说明,此时按哪种优惠方案购买较为合算?
时,通过计算说明,此时按哪种优惠方案购买较为合算?
(4)当![]() 时,你能结合两种优惠方案给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出所需的钱数.
时,你能结合两种优惠方案给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出所需的钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解该校学生的体育锻炼情况,随机抽查了该校部分学生一周的体育锻炼时间的情况,并绘制了如下两幅不完整的统计图:
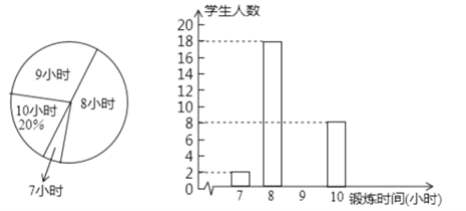
根据以上信息解答以下问题:
(1)本次抽查的学生共有多少名,并补全条形统计图;
(2)写出被抽查学生的体育锻炼时间的众数和中位数;
(3)该校一共有1800名学生,请估计该校学生一周体育锻炼时间不低于9小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4张相同的卡片上分别写有数字-1、-3、4、6,将卡片的背面朝上,并洗匀.
(1)从中任意抽取1张,抽到的数字是奇数的概率是 ;
(2)从中任意抽取1张,并将所取卡片上的数字记作一次函数![]() 中的
中的![]() ;再从余下的卡片中任意抽取1张,并将所取卡片上的数字记作一次函数
;再从余下的卡片中任意抽取1张,并将所取卡片上的数字记作一次函数![]() 中的
中的![]() .利用画树状图或列表的方法,求这个一次函数的图象经过第一、二、四象限的概率.
.利用画树状图或列表的方法,求这个一次函数的图象经过第一、二、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com