
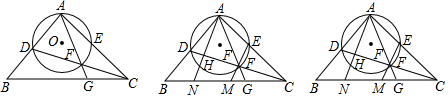
分析 (1)如图1中,作AH⊥CD于H,交BC于N,过点G作GP⊥AG交AN的延长线于P,连接PB、PG.由△ANB∽△GNB,推出$\frac{BN}{PN}$=$\frac{AN}{GN}$,由此$\frac{BN}{AN}$=$\frac{PN}{GN}$,由∠BNP=∠ANG,推出△BNP∽△ANG,推出∠PBN=∠NAG=45°,由△ABP≌△CAD,推出AP=CD,由AP=$\sqrt{2}$AG,即可推出CD=$\sqrt{2}$AG.
(2)如图2中,在图1的基础上,延长BP交EM的延长线于K.由△ABP≌△CAD,推出BP=AD=AE,只要证明四边形APKE是平行四边形,即可推出AE=PK=PB,由PN∥KM,推出$\frac{PB}{PK}$=$\frac{BN}{MN}$=1,即可推出BN=NM.
(3)如图3中,设AF=3a,FG=2a,则AG=PG=5a,AP=CD=5$\sqrt{2}$a,AH=HF=$\frac{3\sqrt{2}}{2}$a,由△ABP∽△CHA,得$\frac{PB}{AP}$=$\frac{AH}{AC}$=$\frac{AB}{CH}$,推出$\frac{2}{5\sqrt{2}a}$=$\frac{\frac{3\sqrt{2}}{2}}{\sqrt{(5\sqrt{2}a)^{2}-{2}^{2}}}$,CH=$\frac{(5\sqrt{2}a)^{2}-{2}^{2}}{\frac{3}{2}\sqrt{2}a}$,整理得225a4-200a2+16=0,解得a=$\sqrt{\frac{4}{45}}$或$\sqrt{\frac{4}{5}}$,推出CF=CH-FH=$\frac{(5\sqrt{2}a)^{2}-{2}^{2}}{\frac{3}{2}\sqrt{2}a}$-$\frac{3}{2}$$\sqrt{2}$a=$\frac{91{a}^{2}-8}{3\sqrt{2}a}$,把a=$\sqrt{\frac{4}{45}}$或$\sqrt{\frac{4}{5}}$代入即可解决问题.
解答 (1)证明:如图1中,作AH⊥CD于H,交BC于N,过点G作GP⊥AG交AN的延长线于P,连接PB、PG.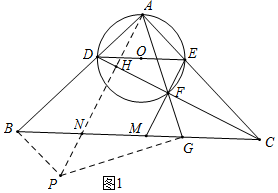
∵∠DAE=90°,AD=AE,
∴∠ADE=∠AED=∠AFH=45°,
∵AH⊥CD,
∴∠AHF=90°,
∴∠HAF=45°=∠APG,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABN=∠GPN,∵∠ANB=∠PNG,
∴△ANB∽△GNB,
∴$\frac{BN}{PN}$=$\frac{AN}{GN}$,
∴$\frac{BN}{AN}$=$\frac{PN}{GN}$,∵∠BNP=∠ANG,
∴△BNP∽△ANG,
∴∠PBN=∠NAG=45°,
∴∠ABP=90°=∠CAD,
∵∠BAP+∠CAH=90°,∠CAH+∠ACD=90°,
∴∠BAP=∠ACD,∵AB=AC,
∴△ABP≌△CAD,
∴AP=CD,
∵AP=$\sqrt{2}$AG,
∴CD=$\sqrt{2}$AG.
(2)证明:如图2中,在图1的基础上,延长BP交EM的延长线于K.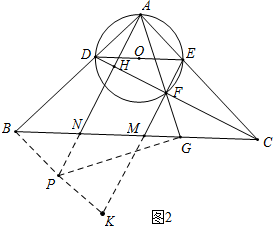
由(1)可知△ABP≌△CAD,
∴BP=AD=AE,
∵∠KBA+∠BAC=180°,
∴AE∥BK,
∵∠DAE=90°,
∴DE是直径,
∴∠DFE=90°,
∴∠AHF+∠DFE=180°,
∴AP∥EK,
∴四边形APKE是平行四边形,
∴AE=PK=PB,
∵PN∥KM,
∴$\frac{PB}{PK}$=$\frac{BN}{MN}$=1,
∴BN=NM.
(3)解:如图3中,设AF=3a,FG=2a,则AG=PG=5a,AP=CD=5$\sqrt{2}$a,AH=HF=$\frac{3\sqrt{2}}{2}$a,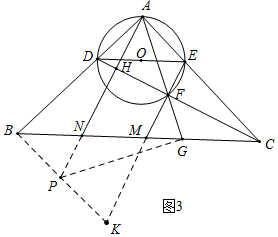
由(2)可知,∵DE=2$\sqrt{2}$,
∴AD=AE=PB=2,
在Rt△ABP中,AB=AC=$\sqrt{(5\sqrt{2}a)^{2}-{2}^{2}}$,
∵∠BAP=∠ACH,∠ABP=∠AHC,
∴△ABP∽△CHA,
∴$\frac{PB}{AP}$=$\frac{AH}{AC}$=$\frac{AB}{CH}$,
∴$\frac{2}{5\sqrt{2}a}$=$\frac{\frac{3\sqrt{2}}{2}}{\sqrt{(5\sqrt{2}a)^{2}-{2}^{2}}}$,CH=$\frac{(5\sqrt{2}a)^{2}-{2}^{2}}{\frac{3}{2}\sqrt{2}a}$,
整理得225a4-200a2+16=0,
∴(45a2-4)(5a2-4)=0,
∵a>0,
∴a=$\sqrt{\frac{4}{45}}$或$\sqrt{\frac{4}{5}}$,
∴CF=CH-FH=$\frac{(5\sqrt{2}a)^{2}-{2}^{2}}{\frac{3}{2}\sqrt{2}a}$-$\frac{3}{2}$$\sqrt{2}$a=$\frac{91{a}^{2}-8}{3\sqrt{2}a}$,
∴把a=$\sqrt{\frac{4}{45}}$或$\sqrt{\frac{4}{5}}$代入得CF=$\frac{2}{45}$$\sqrt{2}$或$\frac{81\sqrt{2}}{4}$.
点评 本题考查圆综合题、等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理、平行四边形的判定、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,学会利用参数构建方程,本题体现了数形结合的数学思想,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | -8、-10 | B. | -8、10 | C. | 8、-10 | D. | 8、10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的有( )
如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2$\sqrt{3}$)2=6 | B. | $\sqrt{1\frac{25}{49}}$=1$\frac{5}{7}$ | ||
| C. | $\sqrt{(-121)×(-9)}$=$\sqrt{121}$×$\sqrt{9}$=33 | D. | $\sqrt{(-4)^{2}}$=±4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{{-1±\sqrt{5}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 最小的有理数是0 | |
| B. | 任何有理数都可以用数轴上的点表示 | |
| C. | 绝对值等于它的相反数的数都是负数 | |
| D. | 整数是正整数和负整数的统称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com