
【题目】某校为了解高一年级住校生在校期间的月生活支出情况,从高一年级600名住校学生中随机抽取部分学生,对他们今年4月份的生活支出情况进行调查统计,并绘制成如下统计图表:

请根据图表中所给的信息,解答下列问题:
(1)在这次调查中共随机抽取了 名学生,图表中的m= ,n= ;
(2)请估计该校高一年级600名住校学生今年4月份生活支出低于350元的学生人数;
(3)现有一些爱心人士有意愿资助该校家庭困难的学生,学校在本次调查的基础上,经过进一步核实,确认高一(2)班有A,B,C三名学生家庭困难,其中A,B为女生,C为男生. 李阿姨申请资助他们中的两名,于是学校让李阿姨从A,B,C三名学生中依次随机抽取两名学生进行资助,请用列表法(或树状图法)求恰好抽到A,B两名女生的概率.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图,AC是□ ABCD的对角线,延长BA至点E,使AE=AB,连接DE.
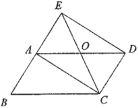
(1)求证:四边形ACDE是平行四边形;
(2)连接EC交AD于点O,若∠EOD=2∠B,求证:四边形ACDE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() .
.
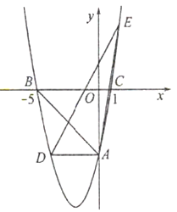
(1)求此抛物线的表达式;
(2)点![]() 是抛物线上一点,且点
是抛物线上一点,且点![]() 关于
关于![]() 轴的对称点在直线
轴的对称点在直线![]() 上,求
上,求![]() 的面积;
的面积;
(3)若点![]() 是直线
是直线![]() 下方的抛物线上一动点,当点
下方的抛物线上一动点,当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的面积最大,求出此时点
的面积最大,求出此时点![]() 的坐标和
的坐标和![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你认真阅读下面的小探究系列,完成所提出的问题.
(1)如图1,将角尺放在正方形ABCD上,使角尺的直角顶点E与正方形ABCD的顶点D重合,角尺的一边交CB于点F,将另一边交BA的延长线于点G.求证:EF=EG.
(2)如图2,移动角尺,使角尺的顶点E始终在正方形ABCD的对角线BD上,其余条件不变,请你思考后直接回答EF和EG的数量关系:EF EG(用“=”或“≠”填空)
(3)运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图3,将(2)中的“正方形ABCD”改成“矩形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,BC=3,求![]() 的值.
的值.
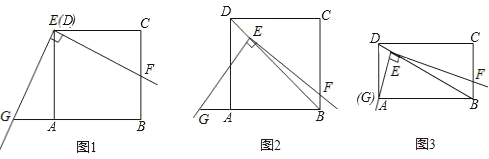
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某木板加工厂将购进的A型、B型两种木板加工成C型,D型两种木板出售,已知一块A型木板的进价比一块B型木板的进价少10元,且购买3块A型木板和2块B型木板共花费120元.
(1)A型木板与B型木板的进价各是多少元?
(2)根据市场需求,该木板加工厂决定用不超过2770元购进A型木板、B型木板共100块,若一块A型木板可制成1块C型木板、2块D型木板;一块B型木板可制成2块C型木板、1块D型木板,且生产出来的C型木板数量不少于D型木板的数量的7/5.
①该木板加工厂有几种进货方案?
②若C型木板每块售价30元,D型木板每块售价25元,且生产出来的C型木板、D型木板全部售出,哪一种方案获得的利润最大,求出最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小乌龟从某点![]() 出发,在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次为(单位:
出发,在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次为(单位:![]() ):+5,-3,+10,-8,-6,+12,-10
):+5,-3,+10,-8,-6,+12,-10
(1)小乌龟最后是否回到出发点![]() ?
?
(2)小乌龟离开原点的距离最远是多少厘米?
(3)小乌龟在爬行过程中,若每爬行![]() 奖励1粒芝麻,则小乌龟一共得到多少粒芝麻?
奖励1粒芝麻,则小乌龟一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩扑克牌游戏,小明背对小亮,让小亮按下列四个步骤操作:
第一步:分发左、中、右三堆牌,每堆牌都为![]() 张,且
张,且![]() ;
;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出五张,放入中间一堆
第四步:左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
(1)填写下表中的空格:
步骤 | 左边一堆牌的张数 | 中间一堆牌的张数 | 右边一堆牌的张数 |
第一步后 |
|
|
|
第二步后 |
|
| |
第三步后 |
|
| |
第四步后 |
|
(2)如若第四步完成后,中间一堆牌的张数的2倍恰好是右边一堆牌的张数的3倍,试求第一步后,每堆牌各有多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,![]() ,
,![]() ,垂足分别为D、F,
,垂足分别为D、F,![]() ,请试说明
,请试说明![]() .
.
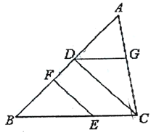
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (____________________________)
(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
又∵![]() (已知)
(已知)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com